Sébastien Labbé

Le 29 octobre dernier, la version 4.7.2 de Sage est sortie. C'est dans cette version de Sage (merci beaucoup à Rob Beezer qui a arbitré cette contribution) qu'a été ajouté le code que j'ai écrit en juin dernier pour résoudre le puzzle appelé Quantumino. Ce puzzle avait été laissé à la salle à manger du Laboratoire de Combinatoire Informatique Mathematique de Montréal par Franco Saliola durant l'hiver 2011...

• Puzzle Quantumino par Family Games America
• Quantumino sur Youtube

La solution utilise le code des liens dansants qui se trouvait déjà dans Sage pour résoudre le problème du Sudoku. Les liens dansants ont été introduits par Donald Knuth en 2000 pour résoudre le pavage d'une région 2D par des pentaminos. Ici nous utilisons la même méthode en dimension quelconque et nous l'appliquons pour résoudre le puzzle Quantumino. Voici les deux pages concernées de la documentation de Sage:

• Tiling Solver
• Quantumino Solver

Voici les 17 blocs de bois du puzzle Quantumino:

sage: from sage.games.quantumino import show_pentaminos
sage: show_pentaminos()

Pour résoudre le puzzle où le pentamino numéroté 7 est mis de côté:

sage: from sage.games.quantumino import QuantuminoSolver
sage: s = QuantuminoSolver(7).solve().next()
sage: s.show3d().show(frame=False)

Pour obtenir d'autres solutions, utilisez l'itérateur retourné par la fonction solve. Notez que trouver la première solution est plus long car on a besoin de créer les données complètes pour décrire le problème:

sage: it = QuantuminoSolver(7).solve()
sage: 1st_solution = it.next()
sage: 2nd_solution = it.next()
sage: 3rd_solution = it.next()
sage: 3rd_solution.show3d().show(frame=False)

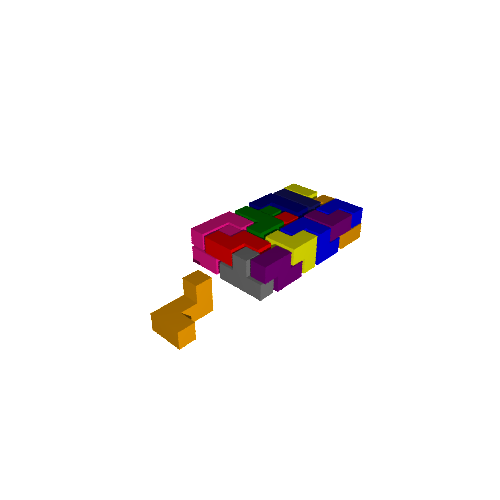
Pour obtenir la solution à l'intérieur d'autres boîtes:

sage: s = QuantuminoSolver(7, box=(4,4,5)).solve().next()
sage: s.show3d()

S'il n'y a pas de solution, l'itération se termine immédiatement:

sage: QuantuminoSolver(7, box=(3,3,3)).solve().next()
Traceback (most recent call last):
...
StopIteration

Si vous êtes patients, vous pouvez essayer de calculer le nombre de solutions. Attention, il y en a beaucoup!:

sage: from sage.games.quantumino import QuantuminoSolver
sage: q = QuantuminoSolver(7)
sage: q.number_of_solutions()   # prendra plusieurs jours de calculs

Le code permet aussi l'introspection. À partir d'un objet de la classe sage.combinat.tiling.TilingSolver, il est possible de récupérer les lignes de la matrice décrivant le problème de couverture exacte en question. Il est également possible d'obtenir une instance du solveur DLX et de tester certaines choses:

sage: q = QuantuminoSolver(0)
sage: T = q.tiling_solver()
sage: T
Tiling solver of 16 pieces into the box (5, 8, 2)
Rotation allowed: True
Reflection allowed: False
Reusing pieces allowed: False
sage: rows = T.rows()
sage: len(rows)
5484
sage: x = T.dlx_solver()
sage: x
<sage.combinat.matrices.dancing_links.dancing_linksWrapper object at ...>