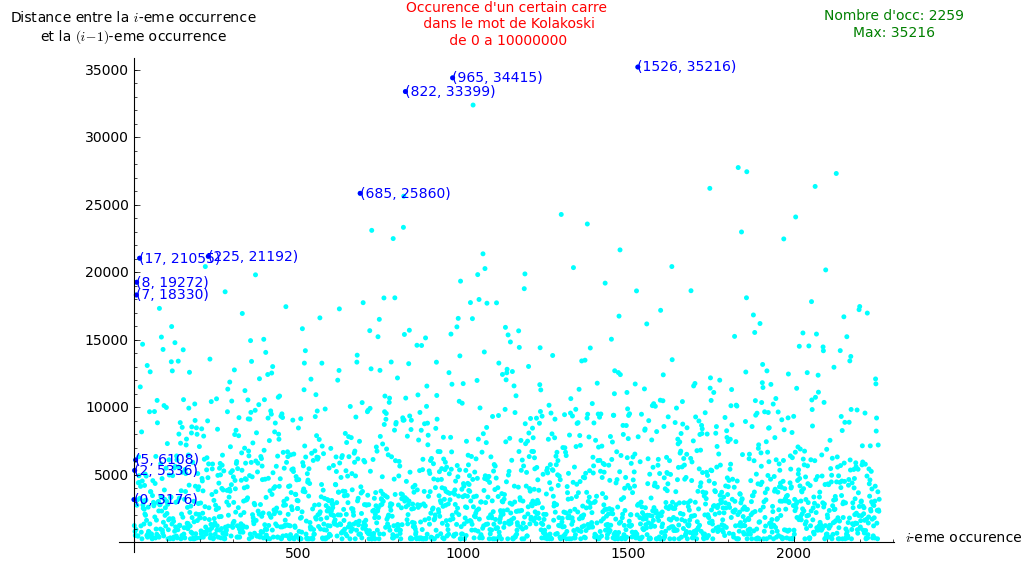
Occurences of a certain factor in the Kolakoski word
16 février 2011 | Catégories: Kolakoski, sage | View CommentsThe factor 212212112112212112122112112212212112112212112122112112 occurs in the Kolakoski word at the positions 3190, 6366, 7614, 12950, 13765, 14277, 20385, 21344, 39674 and so on. The successive gaps of these first eight occurences are 3176, 1248, 5336, 815, 512, 6108, 959, 18330. Are the gap between all of these occurences bounded or not? The following table lists only the gap that are going increasingly for the Kolakoski word up to 100 billion (=10^9).
| i | ith occurence | (i+1)th occurence | gap |
| 0 | 3190 | 6366 | 3176 |
| 2 | 7614 | 12950 | 5336 |
| 5 | 14277 | 20385 | 6108 |
| 7 | 21344 | 39674 | 18330 |
| 8 | 39674 | 58946 | 19272 |
| 17 | 85963 | 107018 | 21055 |
| 225 | 945732 | 966924 | 21192 |
| 685 | 2832810 | 2858670 | 25860 |
| 822 | 3549762 | 3583161 | 33399 |
| 965 | 4188934 | 4223349 | 34415 |
| 1526 | 6773992 | 6809208 | 35216 |
| 7117 | 31279355 | 31320896 | 41541 |
| 18054 | 79167173 | 79213333 | 46160 |
| 20838 | 90761663 | 90809563 | 47900 |
| 176198 | 768146935 | 768195609 | 48674 |
| 292643 | 1278852293 | 1278906094 | 53801 |
| 554207 | 2424441033 | 2424495471 | 54438 |
| 590128 | 2581311276 | 2581367730 | 56454 |
| 948506 | 4150204101 | 4150264753 | 60652 |
| 1156072 | 5055131250 | 5055199553 | 68303 |
| 1514374 | 6620302433 | 6620372047 | 69614 |
| 11154155 | 48788048239 | 48788121823 | 73584 |
The following image draws all the gaps in function of i for the first 10 million digit.