Tiling a polyomino with polyominoes in SageMath
03 décembre 2020 | Catégories: sage, math | View CommentsSuppose that you 3D print many copies of the following 3D hexo-mino at home:
sage: from sage.combinat.tiling import Polyomino, TilingSolver sage: p = Polyomino([(0,0,0), (0,1,0), (1,0,0), (2,0,0), (2,1,0), (2,1,1)], color='blue') sage: p.show3d() Launched html viewer for Graphics3d Object
You would like to know if you can tile a larger polyomino or in particular a rectangular box with many copies of it. The TilingSolver module in SageMath is made for that. See also this recent question on ask.sagemath.org.
sage: T = TilingSolver([p], (7,5,3), rotation=True, reflection=False, reusable=True) sage: T Tiling solver of 1 pieces into a box of size 24 Rotation allowed: True Reflection allowed: False Reusing pieces allowed: True
There is no solution when tiling a box of shape 7x5x3 with this polyomino:
sage: T.number_of_solutions() 0
But there are 4 solutions when tiling a box of shape 4x3x2 with this polyomino:
sage: T = TilingSolver([p], (4,3,2), rotation=True, reflection=False, reusable=True) sage: T.number_of_solutions() 4
We construct the list of solutions:
sage: solutions = [sol for sol in T.solve()]
Each solution contains the isometric copies of the polyominoes tiling the box:
sage: solutions[0] [Polyomino: [(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 1, 0), (2, 0, 0), (2, 1, 0)], Color: #ff0000, Polyomino: [(0, 1, 1), (0, 2, 0), (0, 2, 1), (1, 1, 1), (2, 1, 1), (2, 2, 1)], Color: #ff0000, Polyomino: [(1, 0, 0), (1, 0, 1), (2, 0, 1), (3, 0, 0), (3, 0, 1), (3, 1, 0)], Color: #ff0000, Polyomino: [(1, 2, 0), (1, 2, 1), (2, 2, 0), (3, 1, 1), (3, 2, 0), (3, 2, 1)], Color: #ff0000]
It may be easier to visualize the solutions, so we define the following function allowing to draw the solutions with different colors for each piece:
sage: def draw_solution(solution, size=0.9): ....: colors = rainbow(len(solution)) ....: for piece,col in zip(solution, colors): ....: piece.color(col) ....: return sum((piece.show3d(size=size) for piece in solution), Graphics())
sage: G = [draw_solution(sol) for sol in solutions] sage: G [Graphics3d Object, Graphics3d Object, Graphics3d Object, Graphics3d Object]
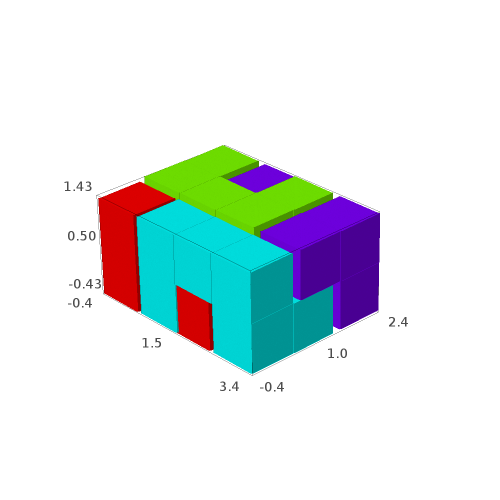
sage: G[0] # in Sage, this will open a 3d viewer automatically
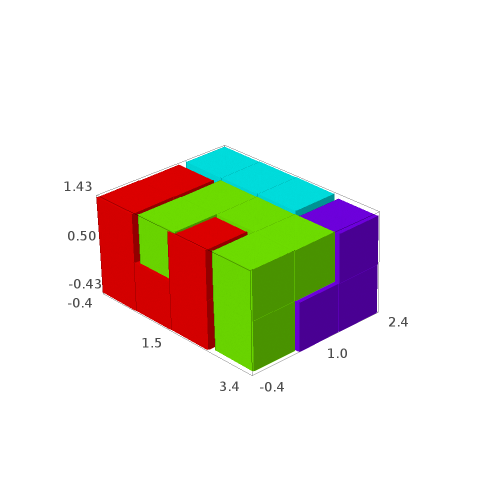
sage: G[1]
sage: G[2]
sage: G[3]
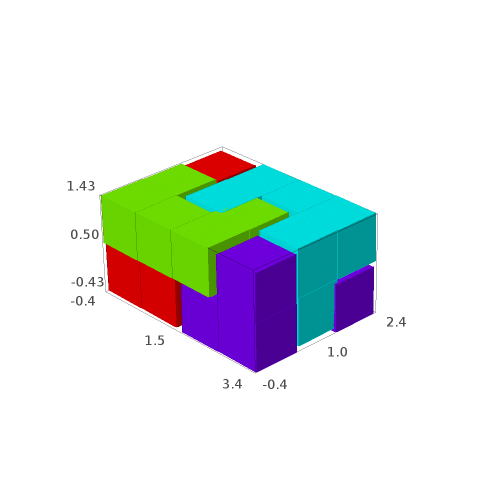
We may save the solutions to a file:
sage: G[0].save('solution0.png', aspect_ratio=1, zoom=1.2) sage: G[1].save('solution1.png', aspect_ratio=1, zoom=1.2) sage: G[2].save('solution2.png', aspect_ratio=1, zoom=1.2) sage: G[3].save('solution3.png', aspect_ratio=1, zoom=1.2)
Question: are all of the 4 solutions isometric to each other?
The tiling problem is solved due to a reduction to the exact cover problem for which dancing links Knuth's algorithm provides all the solutions. One can see the rows of the dancing links matrix as follows:
sage: d = T.dlx_solver() sage: d Dancing links solver for 24 columns and 56 rows sage: d.rows() [[0, 1, 2, 4, 5, 11], [6, 7, 8, 10, 11, 17], [12, 13, 14, 16, 17, 23], ... [4, 6, 7, 9, 10, 11], [10, 12, 13, 15, 16, 17], [16, 18, 19, 21, 22, 23]]
The solutions to the dlx solver can be obtained as follows:
sage: it = d.solutions_iterator() sage: next(it) [3, 36, 19, 52]
These are the indices of the rows each corresponding to an isometric copy of the polyomino within the box.
Since SageMath-9.2, the possibility to reduce the problem to a MILP problem or a SAT instance was added to SageMath (see #29338 and #29955):
sage: d.to_milp() (Boolean Program (no objective, 56 variables, 24 constraints), MIPVariable of dimension 1) sage: d.to_sat_solver() CryptoMiniSat solver: 56 variables, 2348 clauses.
Computer experiments for the Lyapunov exponent for MCF algorithms when dimension is larger than 3
27 mars 2020 | Catégories: sage, slabbe spkg, math | View CommentsIn November 2015, I wanted to share intuitions I developped on the behavior of various distinct Multidimensional Continued Fractions algorithms obtained from various kind of experiments performed with them often involving combinatorics and digitial geometry but also including the computation of their first two Lyapunov exponents.
As continued fractions are deeply related to the combinatorics of Sturmian sequences which can be seen as the digitalization of a straight line in the grid \(\mathbb{Z}^2\), the multidimensional continued fractions algorithm are related to the digitalization of a straight line and hyperplanes in \(\mathbb{Z}^d\).
This is why I shared those experiments in what I called 3-dimensional Continued Fraction Algorithms Cheat Sheets because of its format inspired from typical cheat sheets found on the web. All of the experiments can be reproduced using the optional SageMath package slabbe where I share my research code. People asked me whether I was going to try to publish those Cheat Sheets, but I was afraid the format would change the organization of the information and data in each page, so, in the end, I never submitted those Cheat Sheets anywhere.
Here I should say that \(d\) stands for the dimension of the vector space on which the involved matrices act and \(d-1\) is the dimension of the projective space on which the algorithm acts.
One of the consequence of the Cheat Sheets is that it made us realize that the algorithm proposed by Julien Cassaigne had the same first two Lyapunov exponents as the Selmer algorithm (first 3 significant digits were the same). Julien then discovered the explanation as its algorithm is conjugated to some semi-sorted version of the Selmer algorihm. This result was shared during WORDS 2017 conference. Julien Leroy, Julien Cassaigne and I are still working on the extended version of the paper. It is taking longer mainly because of my fault because I have been working hard on aperiodic Wang tilings in the previous 2 years.
During July 2019, Wolfgang, Valérie and Jörg asked me to perform computations of the first two Lyapunov exponents for \(d\)-dimensional Multidimensional Continued Fraction algorithms for \(d\) larger than 3. The main question of interest is whether the second Lyapunov exponent keeps being negative as the dimension increases. This property is related to the notion of strong convergence almost everywhere of the simultaneous diopantine approximations provided by the algorithm of a fixed vector of real numbers. It did not take me too long to update my package since I had started to generalize my code to larger dimensions during Fall 2017. It turns out that, as the dimension increases, all known MCF algorithms have their second Lyapunov exponent become positive. My computations were thus confirming what they eventually published in their preprint in November 2019.
My motivation for sharing the results is the conference Multidimensional Continued Fractions and Euclidean Dynamics held this week (supposed to be held in Lorentz Center, March 23-27 2020, it got cancelled because of the corona virus) where some discussions during video meetings are related to this subject.
The computations performed below can be summarized in one graphics showing the values of \(1-\theta_2/\theta_1\) with respect to \(d\) for various \(d\)-dimensional MCF algorithms. It seems that \(\theta_2\) is negative up to dimension 10 for Brun, up to dimension 4 for Selmer and up to dimension 5 for ARP.
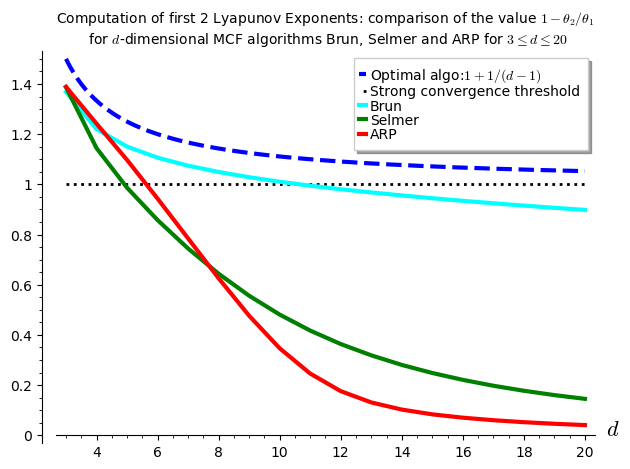
I have to say that I was disapointed by the results because the algorithm Arnoux-Rauzy-Poincaré (ARP) that Valérie and I introduced was not performing so well as its second Lyapunov exponent seems to become positive for dimension \(d\geq 6\). I had good expectations for ARP because it reaches the highest value for \(1-\theta_2/\theta_1\) in the computations performed in the Cheat Sheets, thus better than Brun, better than Selmer when \(d=3\).
The algorithm for the computation of the first two Lyapunov exponents was provided to me by Vincent Delecroix. It applies the algorithm \((v,w)\mapsto(M^{-1}v,M^T w)\) millions of times. The evolution of the size of the vector \(v\) gives the first Lyapunov exponent. The evolution of the size of the vector \(w\) gives the second Lyapunov exponent. Since the computation is performed on 64-bits double floating point number, their are numerical issues to deal with. This is why some Gramm Shimdts operation is performed on the vector \(w\) at each time the vectors are renormalized to keep the vector \(w\) orthogonal to \(v\). Otherwise, the numerical errors cumulate and the computed value for the \(\theta_2\) becomes the same as \(\theta_1\). You can look at the algorithm online starting at line 1723 of the file mult_cont_frac_pyx.pyx from my optional package.
I do not know from where Vincent took that algorithm. So, I do not know how exact it is and whether there exits any proof of lower bounds and upper bounds on the computations being performed. What I can say is that it is quite reliable in the sense that is returns the same values over and over again (by that I mean 3 common most significant digits) with any fixed inputs (number of iterations).
Below, I show the code illustrating how to reproduce the results.
The version 0.6 (November 2019) of my package slabbe includes the necessary code to deal with some \(d\)-dimensional Multidimensional Continued Fraction (MCF) algorithms. Its documentation is available online. It is a PIP package, so it can be installed like this:
sage -pip install slabbe
Recall that the dimension \(d\) below is the linear one and \(d-1\) is the dimension of the space for the corresponding projective algorithm.
Import the Brun, Selmer and Arnoux-Rauzy-Poincaré MCF algorithms from the optional package:
sage: from slabbe.mult_cont_frac import Brun, Selmer, ARP
The computation of the first two Lyapunov exponents performed on one single orbit:
sage: Brun(dim=3).lyapunov_exponents(n_iterations=10^7) (0.30473782969922547, -0.11220958022368056, 1.3682167728713919)
The starting point is taken randomly, but the results of the form of a 3-tuple \((\theta_1,\theta_2,1-\theta_2/\theta_1)\) are about the same:
sage: Brun(dim=3).lyapunov_exponents(n_iterations=10^7) (0.30345018206132324, -0.11171509867725296, 1.3681497170915415)
Increasing the dimension \(d\) yields:
sage: Brun(dim=4).lyapunov_exponents(n_iterations=10^7) (0.32639514522732005, -0.07191456560115839, 1.2203297648654456) sage: Brun(dim=5).lyapunov_exponents(n_iterations=10^7) (0.30918877340506756, -0.0463930802132972, 1.1500477514185734)
It performs an orbit of length \(10^7\) in about .5 seconds, of length \(10^8\) in about 5 seconds and of length \(10^9\) in about 50 seconds:
sage: %time Brun(dim=3).lyapunov_exponents(n_iterations=10^7) CPU times: user 540 ms, sys: 0 ns, total: 540 ms Wall time: 539 ms (0.30488799356325225, -0.11234354880132114, 1.3684748208296182) sage: %time Brun(dim=3).lyapunov_exponents(n_iterations=10^8) CPU times: user 5.09 s, sys: 0 ns, total: 5.09 s Wall time: 5.08 s (0.30455473631148755, -0.11217550411862384, 1.3683262505689446) sage: %time Brun(dim=3).lyapunov_exponents(n_iterations=10^9) CPU times: user 51.2 s, sys: 0 ns, total: 51.2 s Wall time: 51.2 s (0.30438755982577026, -0.11211562816821799, 1.368331834035505)
Here, in what follows, I must admit that I needed to do a small fix to my package, so the code below will not work in version 0.6 of my package, I will update my package in the next days in order that the computations below can be reproduced:
sage: from slabbe.lyapunov import lyapunov_comparison_table
For each \(3\leq d\leq 20\), I compute 30 orbits and I show the most significant digits and the standard deviation of the 30 values computed.
For Brun algorithm:
sage: algos = [Brun(d) for d in range(3,21)] sage: %time lyapunov_comparison_table(algos, n_orbits=30, n_iterations=10^7, ncpus=8) CPU times: user 190 ms, sys: 2.8 s, total: 2.99 s Wall time: 6min 31s Algorithm \#Orbits $\theta_1$ (std) $\theta_2$ (std) $1-\theta_2/\theta_1$ (std) +-------------+----------+--------------------+---------------------+-----------------------------+ Brun (d=3) 30 0.3045 (0.00040) -0.1122 (0.00017) 1.3683 (0.00022) Brun (d=4) 30 0.32632 (0.000055) -0.07188 (0.000051) 1.2203 (0.00014) Brun (d=5) 30 0.30919 (0.000032) -0.04647 (0.000041) 1.1503 (0.00013) Brun (d=6) 30 0.28626 (0.000027) -0.03043 (0.000035) 1.1063 (0.00012) Brun (d=7) 30 0.26441 (0.000024) -0.01966 (0.000027) 1.0743 (0.00010) Brun (d=8) 30 0.24504 (0.000027) -0.01207 (0.000024) 1.04926 (0.000096) Brun (d=9) 30 0.22824 (0.000021) -0.00649 (0.000026) 1.0284 (0.00012) Brun (d=10) 30 0.2138 (0.00098) -0.0022 (0.00015) 1.0104 (0.00074) Brun (d=11) 30 0.20085 (0.000015) 0.00106 (0.000022) 0.9947 (0.00011) Brun (d=12) 30 0.18962 (0.000017) 0.00368 (0.000021) 0.9806 (0.00011) Brun (d=13) 30 0.17967 (0.000011) 0.00580 (0.000020) 0.9677 (0.00011) Brun (d=14) 30 0.17077 (0.000011) 0.00755 (0.000021) 0.9558 (0.00012) Brun (d=15) 30 0.16278 (0.000012) 0.00900 (0.000017) 0.9447 (0.00010) Brun (d=16) 30 0.15556 (0.000011) 0.01022 (0.000013) 0.93433 (0.000086) Brun (d=17) 30 0.149002 (9.5e-6) 0.01124 (0.000015) 0.9246 (0.00010) Brun (d=18) 30 0.14303 (0.000010) 0.01211 (0.000019) 0.9153 (0.00014) Brun (d=19) 30 0.13755 (0.000012) 0.01285 (0.000018) 0.9065 (0.00013) Brun (d=20) 30 0.13251 (0.000011) 0.01349 (0.000019) 0.8982 (0.00014)
For Selmer algorithm:
sage: algos = [Selmer(d) for d in range(3,21)] sage: %time lyapunov_comparison_table(algos, n_orbits=30, n_iterations=10^7, ncpus=8) CPU times: user 203 ms, sys: 2.78 s, total: 2.98 s Wall time: 6min 27s Algorithm \#Orbits $\theta_1$ (std) $\theta_2$ (std) $1-\theta_2/\theta_1$ (std) +---------------+----------+--------------------+---------------------+-----------------------------+ Selmer (d=3) 30 0.1827 (0.00041) -0.0707 (0.00017) 1.3871 (0.00029) Selmer (d=4) 30 0.15808 (0.000058) -0.02282 (0.000036) 1.1444 (0.00023) Selmer (d=5) 30 0.13199 (0.000033) 0.00176 (0.000034) 0.9866 (0.00026) Selmer (d=6) 30 0.11205 (0.000017) 0.01595 (0.000036) 0.8577 (0.00031) Selmer (d=7) 30 0.09697 (0.000012) 0.02481 (0.000030) 0.7442 (0.00032) Selmer (d=8) 30 0.085340 (8.5e-6) 0.03041 (0.000032) 0.6437 (0.00036) Selmer (d=9) 30 0.076136 (5.9e-6) 0.03379 (0.000032) 0.5561 (0.00041) Selmer (d=10) 30 0.068690 (5.5e-6) 0.03565 (0.000023) 0.4810 (0.00032) Selmer (d=11) 30 0.062557 (4.4e-6) 0.03646 (0.000021) 0.4172 (0.00031) Selmer (d=12) 30 0.057417 (3.6e-6) 0.03654 (0.000017) 0.3636 (0.00028) Selmer (d=13) 30 0.05305 (0.000011) 0.03615 (0.000018) 0.3186 (0.00032) Selmer (d=14) 30 0.04928 (0.000060) 0.03546 (0.000051) 0.2804 (0.00040) Selmer (d=15) 30 0.046040 (2.0e-6) 0.03462 (0.000013) 0.2482 (0.00027) Selmer (d=16) 30 0.04318 (0.000011) 0.03365 (0.000014) 0.2208 (0.00028) Selmer (d=17) 30 0.040658 (3.3e-6) 0.03263 (0.000013) 0.1974 (0.00030) Selmer (d=18) 30 0.038411 (2.7e-6) 0.031596 (9.8e-6) 0.1774 (0.00022) Selmer (d=19) 30 0.036399 (2.2e-6) 0.030571 (8.0e-6) 0.1601 (0.00019) Selmer (d=20) 30 0.0346 (0.00011) 0.02955 (0.000093) 0.1452 (0.00019)
For Arnoux-Rauzy-Poincaré algorithm:
sage: algos = [ARP(d) for d in range(3,21)] sage: %time lyapunov_comparison_table(algos, n_orbits=30, n_iterations=10^7, ncpus=8) CPU times: user 226 ms, sys: 2.76 s, total: 2.99 s Wall time: 13min 20s Algorithm \#Orbits $\theta_1$ (std) $\theta_2$ (std) $1-\theta_2/\theta_1$ (std) +--------------------------------+----------+--------------------+---------------------+-----------------------------+ Arnoux-Rauzy-Poincar\'e (d=3) 30 0.4428 (0.00056) -0.1722 (0.00025) 1.3888 (0.00016) Arnoux-Rauzy-Poincar\'e (d=4) 30 0.6811 (0.00020) -0.16480 (0.000085) 1.24198 (0.000093) Arnoux-Rauzy-Poincar\'e (d=5) 30 0.7982 (0.00012) -0.0776 (0.00010) 1.0972 (0.00013) Arnoux-Rauzy-Poincar\'e (d=6) 30 0.83563 (0.000091) 0.0475 (0.00010) 0.9432 (0.00012) Arnoux-Rauzy-Poincar\'e (d=7) 30 0.8363 (0.00011) 0.1802 (0.00016) 0.7845 (0.00020) Arnoux-Rauzy-Poincar\'e (d=8) 30 0.8213 (0.00013) 0.3074 (0.00023) 0.6257 (0.00028) Arnoux-Rauzy-Poincar\'e (d=9) 30 0.8030 (0.00012) 0.4205 (0.00017) 0.4763 (0.00022) Arnoux-Rauzy-Poincar\'e (d=10) 30 0.7899 (0.00011) 0.5160 (0.00016) 0.3467 (0.00020) Arnoux-Rauzy-Poincar\'e (d=11) 30 0.7856 (0.00014) 0.5924 (0.00020) 0.2459 (0.00022) Arnoux-Rauzy-Poincar\'e (d=12) 30 0.7883 (0.00010) 0.6497 (0.00012) 0.1759 (0.00014) Arnoux-Rauzy-Poincar\'e (d=13) 30 0.7930 (0.00010) 0.6892 (0.00014) 0.1309 (0.00014) Arnoux-Rauzy-Poincar\'e (d=14) 30 0.7962 (0.00012) 0.7147 (0.00015) 0.10239 (0.000077) Arnoux-Rauzy-Poincar\'e (d=15) 30 0.7974 (0.00012) 0.7309 (0.00014) 0.08340 (0.000074) Arnoux-Rauzy-Poincar\'e (d=16) 30 0.7969 (0.00015) 0.7411 (0.00014) 0.07010 (0.000048) Arnoux-Rauzy-Poincar\'e (d=17) 30 0.7960 (0.00014) 0.7482 (0.00014) 0.06005 (0.000050) Arnoux-Rauzy-Poincar\'e (d=18) 30 0.7952 (0.00013) 0.7537 (0.00014) 0.05218 (0.000046) Arnoux-Rauzy-Poincar\'e (d=19) 30 0.7949 (0.00012) 0.7584 (0.00013) 0.04582 (0.000035) Arnoux-Rauzy-Poincar\'e (d=20) 30 0.7948 (0.00014) 0.7626 (0.00013) 0.04058 (0.000025)
The computation of the figure shown above is done with the code below:
sage: brun_list = [1.3683, 1.2203, 1.1503, 1.1063, 1.0743, 1.04926, 1.0284, 1.0104, 0.9947, 0.9806, 0.9677, 0.9558, 0.9447, 0.93433, 0.9246, 0.9153, 0.9065, 0.8982] sage: selmer_list = [ 1.3871, 1.1444, 0.9866, 0.8577, 0.7442, 0.6437, 0.5561, 0.4810, 0.4172, 0.3636, 0.3186, 0.2804, 0.2482, 0.2208, 0.1974, 0.1774, 0.1601, 0.1452] sage: arp_list = [1.3888, 1.24198, 1.0972, 0.9432, 0.7845, 0.6257, 0.4763, 0.3467, 0.2459, 0.1759, 0.1309, 0.10239, 0.08340, 0.07010, 0.06005, 0.05218, 0.04582, 0.04058] sage: brun_points = list(enumerate(brun_list, start=3)) sage: selmer_points = list(enumerate(selmer_list, start=3)) sage: arp_points = list(enumerate(arp_list, start=3)) sage: G = Graphics() sage: G += plot(1+1/(x-1), x, 3, 20, legend_label='Optimal algo:$1+1/(d-1)$', linestyle='dashed', color='blue', thickness=3) sage: G += line([(3,1), (20,1)], color='black', legend_label='Strong convergence threshold', linestyle='dotted', thickness=2) sage: G += line(brun_points, legend_label='Brun', color='cyan', thickness=3) sage: G += line(selmer_points, legend_label='Selmer', color='green', thickness=3) sage: G += line(arp_points, legend_label='ARP', color='red', thickness=3) sage: G.ymin(0) sage: G.axes_labels(['$d$','']) sage: G.show(title='Computation of first 2 Lyapunov Exponents: comparison of the value $1-\\theta_2/\\theta_1$\n for $d$-dimensional MCF algorithms Brun, Selmer and ARP for $3\\leq d\\leq 20$')
Comparison of Wang tiling solvers
12 décembre 2018 | Catégories: sage, slabbe spkg, math | View CommentsDuring the last year, I have written a Python module to deal with Wang tiles containing about 4K lines of code including doctests and documentation.
It can be installed like this:
sage -pip install slabbe
It can be used like this:
sage: from slabbe import WangTileSet sage: tiles = [(2,4,2,1), (2,2,2,0), (1,1,3,1), (1,2,3,2), (3,1,3,3), ....: (0,1,3,1), (0,0,0,1), (3,1,0,2), (0,2,1,2), (1,2,1,4), (3,3,1,2)] sage: T0 = WangTileSet([tuple(str(a) for a in t) for t in tiles]) sage: T0.tikz(ncolumns=11).pdf()
The module on wang tiles contains a class WangTileSolver which contains three reductions of the Wang tiling problem the first using MILP solvers, the second using SAT solvers and the third using Knuth's dancing links.
Here is one example of a tiling found using the dancing links reduction:
sage: %time tiling = T0.solver(10,10).solve(solver='dancing_links') CPU times: user 36 ms, sys: 12 ms, total: 48 ms Wall time: 65.5 ms sage: tiling.tikz().pdf()
All these reductions now allow me to compare the efficiency of various types of solvers restricted to the Wang tiling type of problems. Here is the list of solvers that I often use.
| Solver | Description |
|---|---|
| 'Gurobi' | MILP solver |
| 'GLPK' | MILP solver |
| 'PPL' | MILP solver |
| 'LP' | a SAT solver using a reduction to LP |
| 'cryptominisat' | SAT solver |
| 'picosat' | SAT solver |
| 'glucose' | SAT solver |
| 'dancing_links' | Knuth's algorihm |
In this recent work on the substitutive structure of Jeandel-Rao tilings, I introduced various Wang tile sets \(T_i\) for \(i\in\{0,1,\dots,12\}\). In this blog post, we will concentrate on the 11 Wang tile set \(T_0\) introduced by Jeandel and Rao as well as \(T_2\) containing 20 tiles and \(T_3\) containing 24 tiles.
Tiling a n x n square
The most natural question to ask is to find valid Wang tilings of \(n\times n\) square with given Wang tiles. Below is the time spent by each mentionned solvers to find a valid tiling of a \(n\times n\) square in less than 10 seconds for each of the three wang tile sets \(T_0\), \(T_2\) and \(T_3\).
We remark that MILP solvers are slower. Dancing links can solve 20x20 squares with Jeandel Rao tiles \(T_0\) and SAT solvers are performing very well with Glucose being the best as it can find a 55x55 tiling with Jeandel-Rao tiles \(T_0\) in less than 10 seconds.
Finding all dominoes allowing a surrounding of given radius
One thing that is often needed in my research is to enumerate all horizontal and vertical dominoes that allow a given surrounding radius. This is a difficult question in general as deciding if a given tile set admits a tiling of the infinite plane is undecidable. But in some cases, the information we get from the dominoes admitting a surrounding of radius 1, 2, 3 or 4 is enough to conclude that the tiling can be desubstituted for instance. This is why we need to answer this question as fast as possible.
Below is the comparison in the time taken by each solver to compute all vertical and horizontal dominoes allowing a surrounding of radius 1, 2 and 3 (in less than 1000 seconds for each execution).
What is surprising at first is that the solvers that performed well in the first \(n\times n\) square experience are not the best in the second experiment computing valid dominoes. Dancing links and the MILP solver Gurobi are now the best algorithms to compute all dominoes. They are followed by picosat and cryptominisat and then glucose.
The source code of the above comparisons
The source code of the above comparison can be found in this Jupyter notebook. Note that it depends on the use of Glucose as a Sage optional package (#26361) and on the most recent development version of slabbe optional Sage Package.
Wooden laser-cut Jeandel-Rao tiles
07 septembre 2018 | Catégories: sage, slabbe spkg, math, découpe laser | View CommentsI have been working on Jeandel-Rao tiles lately.
Before the conference Model Sets and Aperiodic Order held in Durham UK (Sep 3-7 2018), I thought it would be a good idea to bring some real tiles at the conference. So I first decided of some conventions to represent the above tiles as topologically closed disk basically using the representation of integers in base 1:
With these shapes, I created a 33 x 19 patch. With 3cm on each side, the patch takes 99cm x 57cm just within the capacity of the laser cut machine (1m x 60 cm):
With the help of David Renault from LaBRI, we went at Coh@bit, the FabLab of Bordeaux University and we laser cut two 3mm thick plywood for a total of 1282 Wang tiles. This is the result:
One may recreate the 33 x 19 tiling as follows (note that I am using Cartesian-like coordinates, so the first list data[0] actually is the first column from bottom to top):
sage: data = [[10, 4, 6, 1, 3, 3, 7, 0, 9, 7, 2, 6, 1, 3, 8, 7, 0, 9, 7], ....: [4, 5, 6, 1, 8, 10, 4, 0, 9, 3, 8, 7, 0, 9, 7, 5, 0, 9, 3], ....: [3, 7, 6, 1, 7, 2, 5, 0, 9, 8, 7, 5, 0, 9, 3, 7, 0, 9, 10], ....: [10, 4, 6, 1, 3, 8, 7, 0, 9, 7, 5, 6, 1, 8, 10, 4, 0, 9, 3], ....: [2, 5, 6, 1, 8, 7, 5, 0, 9, 3, 7, 6, 1, 7, 2, 5, 0, 9, 8], ....: [8, 7, 6, 1, 7, 5, 6, 1, 8, 10, 4, 6, 1, 3, 8, 7, 0, 9, 7], ....: [7, 5, 6, 1, 3, 7, 6, 1, 7, 2, 5, 6, 1, 8, 7, 5, 0, 9, 3], ....: [3, 7, 6, 1, 10, 4, 6, 1, 3, 8, 7, 6, 1, 7, 5, 6, 1, 8, 10], ....: [10, 4, 6, 1, 3, 3, 7, 0, 9, 7, 5, 6, 1, 3, 7, 6, 1, 7, 2], ....: [2, 5, 6, 1, 8, 10, 4, 0, 9, 3, 7, 6, 1, 10, 4, 6, 1, 3, 8], ....: [8, 7, 6, 1, 7, 5, 5, 0, 9, 10, 4, 6, 1, 3, 3, 7, 0, 9, 7], ....: [7, 5, 6, 1, 3, 7, 6, 1, 10, 4, 5, 6, 1, 8, 10, 4, 0, 9, 3], ....: [3, 7, 6, 1, 10, 4, 6, 1, 3, 3, 7, 6, 1, 7, 2, 5, 0, 9, 8], ....: [10, 4, 6, 1, 3, 3, 7, 0, 9, 10, 4, 6, 1, 3, 8, 7, 0, 9, 7], ....: [4, 5, 6, 1, 8, 10, 4, 0, 9, 3, 3, 7, 0, 9, 7, 5, 0, 9, 3], ....: [3, 7, 6, 1, 7, 2, 5, 0, 9, 8, 10, 4, 0, 9, 3, 7, 0, 9, 10], ....: [10, 4, 6, 1, 3, 8, 7, 0, 9, 7, 5, 5, 0, 9, 10, 4, 0, 9, 3], ....: [2, 5, 6, 1, 8, 7, 5, 0, 9, 3, 7, 6, 1, 10, 4, 5, 0, 9, 8], ....: [8, 7, 6, 1, 7, 5, 6, 1, 8, 10, 4, 6, 1, 3, 3, 7, 0, 9, 7], ....: [7, 5, 6, 1, 3, 7, 6, 1, 7, 2, 5, 6, 1, 8, 10, 4, 0, 9, 3], ....: [3, 7, 6, 1, 10, 4, 6, 1, 3, 8, 7, 6, 1, 7, 2, 5, 0, 9, 8], ....: [10, 4, 6, 1, 3, 3, 7, 0, 9, 7, 2, 6, 1, 3, 8, 7, 0, 9, 7], ....: [4, 5, 6, 1, 8, 10, 4, 0, 9, 3, 8, 7, 0, 9, 7, 5, 0, 9, 3], ....: [3, 7, 6, 1, 7, 2, 5, 0, 9, 8, 7, 5, 0, 9, 3, 7, 0, 9, 10], ....: [10, 4, 6, 1, 3, 8, 7, 0, 9, 7, 5, 6, 1, 8, 10, 4, 0, 9, 3], ....: [3, 3, 7, 0, 9, 7, 5, 0, 9, 3, 7, 6, 1, 7, 2, 5, 0, 9, 8], ....: [8, 10, 4, 0, 9, 3, 7, 0, 9, 10, 4, 6, 1, 3, 8, 7, 0, 9, 7], ....: [7, 5, 5, 0, 9, 10, 4, 0, 9, 3, 3, 7, 0, 9, 7, 5, 0, 9, 3], ....: [3, 7, 6, 1, 10, 4, 5, 0, 9, 8, 10, 4, 0, 9, 3, 7, 0, 9, 10], ....: [10, 4, 6, 1, 3, 3, 7, 0, 9, 7, 5, 5, 0, 9, 10, 4, 0, 9, 3], ....: [2, 5, 6, 1, 8, 10, 4, 0, 9, 3, 7, 6, 1, 10, 4, 5, 0, 9, 8], ....: [8, 7, 6, 1, 7, 5, 5, 0, 9, 10, 4, 6, 1, 3, 3, 7, 0, 9, 7], ....: [7, 5, 6, 1, 3, 7, 6, 1, 10, 4, 5, 6, 1, 8, 10, 4, 0, 9, 3]]
The above patch have been chosen among 1000 other randomly generated as the closest to the asymptotic frequencies of the tiles in Jeandel-Rao tilings (or at least in the minimal subshift that I describe in the preprint):
sage: from collections import Counter sage: c = Counter(flatten(data)) sage: tile_count = [c[i] for i in range(11)]
The asymptotic frequencies:
sage: phi = golden_ratio.n() sage: Linv = [2*phi + 6, 2*phi + 6, 18*phi + 10, 2*phi + 6, 8*phi + 2, ....: 5*phi + 4, 2*phi + 6, 12/5*phi + 14/5, 8*phi + 2, ....: 2*phi + 6, 8*phi + 2] sage: perfect_proportions = vector([1/a for a in Linv])
Comparison of the number of tiles of each type with the expected frequency:
sage: header_row = ['tile id', 'Asymptotic frequency', 'Expected nb of copies', ....: 'Nb copies in the 33x19 patch'] sage: columns = [range(11), perfect_proportions, vector(perfect_proportions)*33*19, tile_count] sage: table(columns=columns, header_row=header_row) tile id Asymptotic frequency Expected nb of copies Nb copies in the 33x19 patch +---------+----------------------+-----------------------+------------------------------+ 0 0.108271182329550 67.8860313206280 67 1 0.108271182329550 67.8860313206280 65 2 0.0255593590340479 16.0257181143480 16 3 0.108271182329550 67.8860313206280 71 4 0.0669152706817991 41.9558747174880 42 5 0.0827118232955023 51.8603132062800 51 6 0.108271182329550 67.8860313206280 65 7 0.149627093977301 93.8161879237680 95 8 0.0669152706817991 41.9558747174880 44 9 0.108271182329550 67.8860313206280 67 10 0.0669152706817991 41.9558747174880 44
I brought the \(33\times19=641\) tiles at the conference and offered to the first 7 persons to find a \(7\times 7\) tiling the opportunity to keep the 49 tiles they used. 49 is a good number since the frequency of the lowest tile (with id 2) is about 2% which allows to have at least one copy of each tile in a subset of 49 tiles allowing a solution.
A natural question to ask is how many such \(7\times 7\) tilings does there exist? With ticket #25125 that was merged in Sage 8.3 this Spring, it is possible to enumerate and count solutions in parallel with Knuth dancing links algorithm. After the installation of the Sage Optional package slabbe (sage -pip install slabbe), one may compute that there are 152244 solutions.
sage: from slabbe import WangTileSet sage: tiles = [(2,4,2,1), (2,2,2,0), (1,1,3,1), (1,2,3,2), (3,1,3,3), ....: (0,1,3,1), (0,0,0,1), (3,1,0,2), (0,2,1,2), (1,2,1,4), (3,3,1,2)] sage: T0 = WangTileSet(tiles) sage: T0_solver = T0.solver(7,7) sage: %time T0_solver.number_of_solutions(ncpus=8) CPU times: user 16 ms, sys: 82.3 ms, total: 98.3 ms Wall time: 388 ms 152244
One may also get the list of all solutions and print one of them:
sage: %time L = T0_solver.all_solutions(); print(len(L)) 152244 CPU times: user 6.46 s, sys: 344 ms, total: 6.8 s Wall time: 6.82 s sage: L[0] A wang tiling of a 7 x 7 rectangle sage: L[0].table() # warning: the output is in Cartesian-like coordinates [[1, 8, 10, 4, 5, 0, 9], [1, 7, 2, 5, 6, 1, 8], [1, 3, 8, 7, 6, 1, 7], [0, 9, 7, 5, 6, 1, 3], [0, 9, 3, 7, 6, 1, 8], [1, 8, 10, 4, 6, 1, 7], [1, 7, 2, 2, 6, 1, 3]]
This is the number of distinct sets of 49 tiles which admits a 7x7 solution:
sage: from collections import Counter sage: def count_tiles(tiling): ....: C = Counter(flatten(tiling.table())) ....: return tuple(C.get(a,0) for a in range(11)) sage: Lfreq = map(count_tiles, L) sage: Lfreq_count = Counter(Lfreq) sage: len(Lfreq_count) 83258
Number of other solutions with the same set of 49 tiles:
sage: Counter(Lfreq_count.values()) Counter({1: 49076, 2: 19849, 3: 6313, 4: 3664, 6: 1410, 5: 1341, 7: 705, 8: 293, 9: 159, 14: 116, 10: 104, 12: 97, 18: 44, 11: 26, 15: 24, 13: 10, 17: 8, 22: 6, 32: 6, 16: 3, 28: 2, 19: 1, 21: 1})
How the number of \(k\times k\)-solutions grows for k from 0 to 9:
sage: [T0.solver(k,k).number_of_solutions() for k in range(10)] [0, 11, 85, 444, 1723, 9172, 50638, 152244, 262019, 1641695]
Unfortunately, most of those \(k\times k\)-solutions are not extendable to a tiling of the whole plane. Indeed the number of \(k\times k\) patches in the language of the minimal aperiodic subshift that I am able to describe and which is a proper subset of Jeandel-Rao tilings seems, according to some heuristic, to be something like:
[1, 11, 49, 108, 184, 268, 367, 483]
I do not share my (ugly) code for this computation yet, as I will rather share clean code soon when times come. So among the 152244 about only 483 (0.32%) of them are prolongable into a uniformly recurrent tiling of the plane.
Conférence sur les pavages
27 juin 2016 | Catégories: math | View CommentsRécemment, j'ai manqué quelques entraînements d'ultimate à Liège, car je participais à une conférence sur les pavages en France. "Les pavages?" me demande Maïté qui vient de commencer des travaux dans sa nouvelle maison. Et oui, les pavages! Mais pourquoi s'intéresser aux pavages?
Les pavages sont utiles en chimie et en physique, car ils permettent de modéliser mathématiquement le placement des atomes et molécules dans l'espace. Dans un cristal, les atomes sont placés de manière périodique comme la plupart des pavages utilisés dans les salles de bain de nos maisons.
Dans les années 80, Daniel Schechtman, un chercheur en chimie, a découvert des cristaux qui n'ont pas de structure périodique. Au début et pendant plusieurs années, ses collègues ne l'ont pas cru. Il a finalement obtenu le prix Nobel de Chimie en 2011 pour sa découverte.
Or on connaissait depuis les années 70 des pavages apériodique du plan. Les plus connus sont les pavages de Penrose qui ont plusieurs variantes. Avec la découverte des quasi-cristaux, les pavages apériodiques ont continué de susciter l'intérêt des chercheurs jusqu'à aujourd'hui...
Quelques liens:
- Le prix Nobel de Chimie 2011 (pdf, document de vulgarisation, belles images en page 5)
- l'article sur Images des mathématiques rédigé par Thierry de la Rue et Elise Janvresse
- Les pavages de Penrose (wikipédia) pour inspirer dans la conception d'une future salle de bain:)
« Previous Page -- Next Page »
Propulsé par Blogofile
S'abonner au Flux RSS
et aux Commentaires.
This work by Sébastien Labbé is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.