Aujourd'hui avait lieu une rencontre de l'ANR DynA3S. Suite à une présentation de Brigitte Vallée, j'ai codé quelques lignes en Sage pour étudier une fonction qu'elle a introduite. Cette fonction est reliée à la compréhension de la densité des termes sous-diagonaux dans l'exécution de l'algorithme LLL.

D'abord voici mon fichier: brigitte.sage.

Pour utiliser ce fichier, il faut d'abord l'importer dans Sage en utilisant la commande suivante. En ligne de commande, ça fonctionne bien. Dans le Sage notebook, je ne sais plus trop si la commande load permet encore de le faire (?):

sage: %runfile brigitte.sage       # not tested

On doit générer plusieurs orbites pour visualiser quelque chose, car les orbites de la fonction sont de taille 1, 2 ou 3 en général avant que la condition d'arrêt soit atteinte. Ici, on génère 10000 orbites (les points initiaux sont choisis aléatoirement et uniformément dans \([0,1]\times[-0.5, 0.5]\). On dessine les derniers points des orbites:

sage: D = plusieurs_orbit(10000)
Note: la plus longue orbite est de taille 3
sage: A = points(D[0], color='red', legend_label='derniers')
sage: B = points(D[1], color='blue', legend_label='avant derniers')
sage: C = points(D[2], color='black', legend_label='2e avant derniers')
sage: G = A + B + C
sage: G.axes_labels(("$x$", r"$\nu$"))
sage: title = r"$(x,\nu) \mapsto (\frac{x}{(x+\nu^2)^2},\frac{\nu}{(x+\nu^2)})$"
sage: G.show(title=title, xmax=2)

Un raccourci pour faire à peu près le même dessin que ci-haut:

sage: draw_plusieurs_orbites(10000).show(xmax=2)

On dessine des histogrammes surperposés de la densité de ces points une fois projetés sur l'axe des \(\nu\):

sage: histogrammes_nu(10000, nbox=10)

Le dessin semble indiquer que la densité non uniforme semble provenir simplement par les points \((x,\nu)\) tels que \(x\leq 1\).

On dessine des histogrammes superposés de la densité de ces points une fois projetés sur l'axe des \(x\) (on donne des couleurs selon la valeur de \(\nu\)):

sage: histogrammes_x(30000, nbox=5, ymax=1500, xmax=8)

Le dessin semble indiquer que la densité ne dépend pas de \(\nu\) pour \(x\geq 1\).

(NEW: See also the demo I made at the Sage Paris group meeting in March 2014.)

Ticket #12719 (Upgrade to IPython 0.13) was merged into sage-5.7.beta1. This took a lot of energy (see the number of comments in the ticket and especially the number of patches and dependencies). Big thanks to Volker Braun, Mike Hansen, Jason Grout, Jeroen Demeyer who worked on this since almost one year. Note that in December 2012, the IPython project has received a $1.15M grant from the Alfred P. Sloan foundation, that will support IPython development for the next two years. I really like this IPython sage command line interface so it is really good news!

The IPython notebook

Since version 0.12 (December 21 2011), IPython is released with its own notebook. The differences with the Sage Notebook are explained by Fernando Perez, leader of IPython project, in the blog post The IPython notebook: a historical retrospective he wrote in January 2012. One of the differences is that the IPython Notebook run in its own directory whereas each cell of the Sage Notebook lives in its directory. As William Stein says in the presentation Browser-based notebook interfaces for mathematical software - past, present and future he gave last December at ICERM, there are plenty of projects and directions these days for those interfaces.

In May 2012, I tested the same ticket which was to upgrade to IPython 0.12 at that time. Today, I was curious to test it again.

First, I installed sage-5.7.beta4:

./sage -version
Sage Version 5.7.beta4, Release Date: 2013-02-09

Install tornado:

./sage -sh
easy_install-2.7 tornado

[update March 6th, 2014] Note that some linux user have to install libssl-dev before tornado:

sudo apt-get install libssl-dev

Install zeromq and pyzmq:

./sage -i zeromq
./sage -i pyzmq

Start the ipython notebook:

./sage -ipython notebook
[NotebookApp] Using existing profile dir: u'/Users/slabbe/.sage/ipython-0.12/profile_default'
[NotebookApp] Serving notebooks from /Users/slabbe/Applications/sage-5.7.beta4
[NotebookApp] The IPython Notebook is running at: http://127.0.0.1:8888/
[NotebookApp] Use Control-C to stop this server and shut down all kernels.

Create a new notebook. One may use sage commands by adding the line from sage.all import * in the first cell.

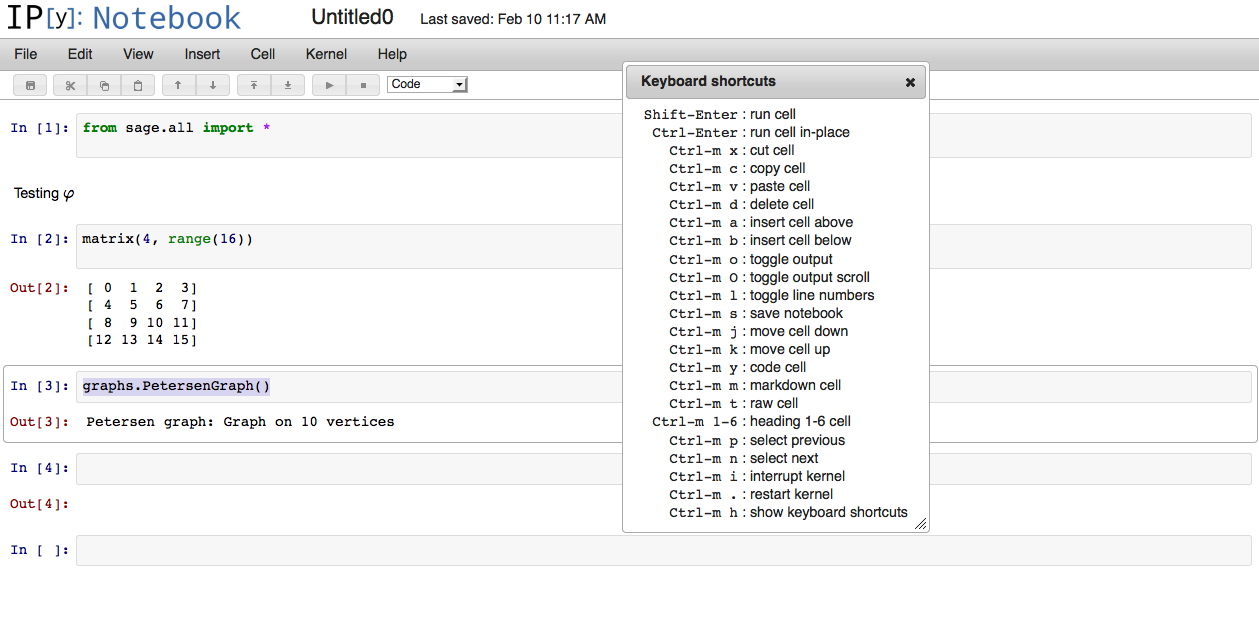
The next things I want to look at are:

• Test the conversion of files from .py to .pynb.
• Test the conversion of files from .rst to .pynb.
• Test the qtconsole.
• Test the parallel computing capacities of the IPython.

Since Sage Days 20 at Marseille held in January 2010, I have been doing the same example over and over again each time I showed someone else how object oriented coding works in Python: using fruits, strawberry, oranges and bananas.

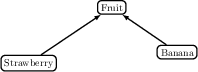
Here is my file: fruit.py. I use to build it from scratch by adding one line at a time using attach command to see what has changed starting with Banana class, then Strawberry class then Fruit class which gathers all common methods.

This time, I wrote the complete documentation (all tests pass, coverage is 100%) and followed Sage coding convention as far as I know them. Thus, I hope this file can be useful as an example to explain those coding convention to newcomers.

One may check that all tests pass using:

$ sage -t fruit.py
sage -t  "fruit.py"
[3.7 s]

----------------------------------------------------------------------
All tests passed!
Total time for all tests: 3.8 seconds

One may check that documentation and doctest coverage is 100%:

$ sage -coverage fruit.py
----------------------------------------------------------------------
fruit.py
SCORE fruit.py: 100% (10 of 10)
----------------------------------------------------------------------

This message is about differences between a Python function and a symbolic function. This is also explained in the Some Common Issues with Functions page in the Sage Tutorial.

In Sage, one may define a symbolic function like:

sage: f(x) = x^2-1

And draw it using one the following way (both works):

sage: plot(f, (x,-10,10))
sage: plot(f(x), (x,-10,10))

Here both f and f(x) are symbolic expressions:

sage: type(f)
<type 'sage.symbolic.expression.Expression'>
sage: type(f(x))
<type 'sage.symbolic.expression.Expression'>

although there are different:

sage: f
x |--> x^2 - 1
sage: f(x)
x^2 - 1

Now if f is a Python function defined with a def statement:

sage: def f(x):
....:     if x>0:
....:         return x
....:     else:
....:         return 0

It is really a Python function:

sage: f
<function f at 0xb933470>
sage: type(f)
<type 'function'>

As above, one can draw the function f:

sage: plot(f, (x,-10,10))

But be carefull, drawing f(x) will not work as expected:

sage: plot(f(x), (x,-10,10))

Why? Because, the python function f gets evaluated on the variable x and this may either raise an exception depending on the definition of f or return some result which might not be a symbolic expression. Here f(x) gets always evaluated to zero because in the definition of f, bool(x > 0) returns False:

sage: x
x
sage: bool(x > 0)
False
sage: f(x)
0

Hence the following constant function is drawn:

sage: plot(0, (x,-10,10))

which is not what we want.

Today, I am presenting the Chapter 3 of the book Probability on Graphs of Geoffrey Grimmett during a monthly reading seminar at LIAFA. The title of the chapter is Percolation and self-avoiding walks. I did some computations to improve my intuition on the question. My code is in the following file : bond_percolation.sage. This post is about some of my computations. You might want to test them yourself online using the Sage Cell Server.

Some samples when p=0.5

A bond percolation sample inside the box \(\Lambda(m)=[-m,m]^d\) when \(p=0.5\) and \(d=2\):

sage: S = BondPercolationSample(p=0.5, d=2)
sage: S.plot(m=40, pointsize=10, thickness=1)
Graphics object consisting of 7993 graphics primitives
sage: _.show()

Another time gives something different:

sage: S = BondPercolationSample(p=0.5, d=2)
sage: S.plot(m=40, pointsize=10, thickness=1)
Graphics object consisting of 10176 graphics primitives
sage: _.show()

Some samples for ranges of values of p

From p=0.1 to p=0.9:

sage: percolation_graphics_array(srange(0.1,1,0.1), d=2, m=5)

From p=0.41 to p=0.49:

sage: percolation_graphics_array(srange(0.41,0.50,0.01), d=2, m=5)

From p=0.51 to p=0.59:

sage: percolation_graphics_array(srange(0.51,0.60,0.01), d=2, m=5)

Upper bound and lower bound for percolation probability \(\Theta(p)\)

In every case, we have the following upper bound for the percolation probability: \[ \Theta(p) = \mathbb{P}_p(\vert C_0\vert=\infty) \leq \mathbb{P}_p(\vert C_0\vert > 1) = 1 - \mathbb{P}_p(\vert C_0\vert = 1) = 1 - (1-p)^{2d}. \] In particular, if \(p\neq 1\), then \(\Theta(p)<1\). In Sage, define the upper bound:

sage: p,n = var('p,n')
sage: d = var('d')
sage: upper_bound = 1 - (1-p)^(2*d)

Also, from Equation (3.8), we have the following lower bound: \[ \Theta(p) \geq 1 - \sum_{n=4}^{\infty} n (4(1-p))^n. \]

In Sage, define the lower bound:

sage: p,n = var('p,n')
sage: lower_bound = 1 - sum(n*(4*(1-p))^n,n,4,oo)
sage: lower_bound.factor()
-(3072*p^5 - 14336*p^4 + 26624*p^3 - 24592*p^2 + 11288*p - 2057)/(4*p - 3)^2

This is not defined when \(p=3/4\), but we are interested in the values in the interval \(]3/4,1]\). In particular, for which value of \(p\) is this lower bound strictly larger than zero:

sage: root = lower_bound.find_root(0.76, 0.99); root
0.8639366490304586

Let's now draw a graph of the lower and upper bound:

sage: U = plot(upper_bound(d=2),(0,1),color='red', thickness=3)
sage: L = plot(lower_bound,(0.86,1),color='green', thickness=3)
sage: G = U + L
sage: G += point((root, 0), color='red', size=20)
sage: lower = r"$1-\sum_{n=4}^{\infty} n4^n(1-p)^n$"
sage: upper = r"$1 -(1-p)^{4}$"
sage: title = r"$1-\sum_{n=4}^{\infty} n4^n(1-p)^n\leq\Theta(p)\leq 1 -(1-p)^{2d}$"
sage: G += text(title, (.5, 1.05), color='black', fontsize=15)
sage: G += text(upper, (.3, 0.5), color='red', fontsize=20)
sage: G += text(lower, (.7, 0.5), color='green', fontsize=20)
sage: G += text("%.5f"%root,(0.88, .03), color='green', horizontal_alignment='left')
sage: G.show()

Thus we conclude that \(\Theta(p) >0\) for \(p>0.8639\) and thus \(p_c \leq 0.8639\).

Percolation probability - dimension 2

The code allows to define the percolation probability function for a given dimension d. It generates n samples and consider the cluster to be infinite if its cardinality is larger than the given stop value.

Here we use Sage adaptative recursion algorithm for drawing the plot of the percolation probability which finds the particular important intervals to ask for more values of the function. See help section of plot function for details. Because T might be long to compute we start with only 4 points.

When stop=100:

sage: T = PercolationProbability(d=2, n=10, stop=100)
sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

When stop=1000:

sage: T = PercolationProbability(d=2, n=10, stop=1000)
sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

When stop=2000:

sage: T = PercolationProbability(d=2, n=10, stop=2000)
sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

Percolation probability - dimension 3

When stop=100:

sage: T = PercolationProbability(d=3, n=10, stop=100)
sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

When stop=1000:

sage: T = PercolationProbability(d=3, n=10, stop=1000)
sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

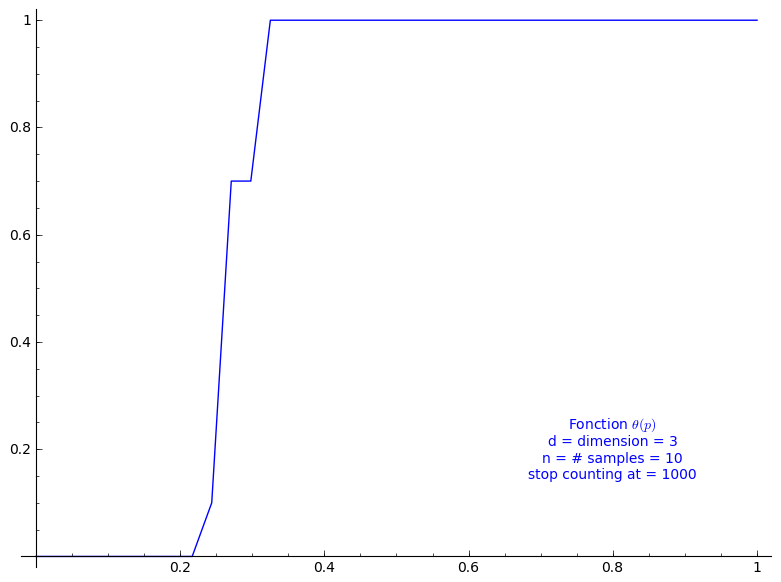
Percolation probability - dimension 4

When stop=100:

sage: T = PercolationProbability(d=4, n=10, stop=100)
sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

Percolation probability - dimension 13

When stop=100:

sage: T = PercolationProbability(d=13, n=10, stop=100)
sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

sage: L = [1, 4, 12, 36, 100, 284, 780, 2172, 5916, 16268, 44100, 120292,
324932, 881500, 2374444, 6416596, 17245332, 46466676, 124658732, 335116620,
897697164, 2408806028, 6444560484, 17266613812, 46146397316, 123481354908,
329712786220, 881317491628]
sage: for k in range(1, len(L)): print numerical_approx(L[k]^(1/k))
4.00000000000000
3.46410161513775
3.30192724889463
3.16227766016838
3.09502148400370
3.03400133198980
2.99705187539871
2.96144397263395
2.93714926770637
2.91369345857619
2.89627439045790
2.87949308754677
2.86632078916860
2.85362749495679
2.84328447096562
2.83329615650289
2.82493415671599
2.81684125361654
2.80992368218258
2.80321554383456
2.79738645741910
2.79172363211806
2.78673687369245
2.78188437392354
2.77756387722633
2.77335345579129
2.76956977331575

sage: L = [1, 6, 30, 150, 726, 3534, 16926, 81390, 387966, 1853886,
8809878, 41934150, 198842742, 943974510, 4468911678, 21175146054,
100121875974, 473730252102, 2237723684094, 10576033219614, 49917327838734,
235710090502158, 1111781983442406, 5245988215191414, 24730180885580790,
116618841700433358, 549493796867100942,2589874864863200574,
12198184788179866902, 57466913094951837030, 270569905525454674614]
sage: for k in range(1, len(L)): print numerical_approx(L[k]^(1/k))
6.00000000000000
5.47722557505166
5.31329284591305
5.19079831727404
5.12452137580198
5.06709510955294
5.02933019629493
4.99573287588832
4.97111339009676
4.94876680377358
4.93129192790635
4.91521453865211
4.90209314463520
4.88990167518413
4.87964724632057
4.87004597517131
4.86178722582108
4.85400655861169
4.84719703702142
4.84074902256992
4.83502763526502
4.82958688248615
4.82470487210973
4.82004549244633
4.81582557693112
4.81178552451599
4.80809774735294
4.80455755518719
4.80130435575213
4.79817388859565

sage: k < 2.76956977331575
k < 2.76956977331575
sage: _ / (2.76956977331575  * k)
0.361066909970928 < (1/k)
sage: 1 - 0.361066909970928
0.638933090029072

sage: k < 4.79817388859565
k < 4.79817388859565
sage: _ / (4.79817388859565 * k)
0.208412621805310 < (1/k)