Percolation and self-avoiding walks
18 décembre 2012 | Mise à jour: 20 décembre 2012 | Catégories: sage | View CommentsToday, I am presenting the Chapter 3 of the book Probability on Graphs of Geoffrey Grimmett during a monthly reading seminar at LIAFA. The title of the chapter is Percolation and self-avoiding walks. I did some computations to improve my intuition on the question. My code is in the following file : bond_percolation.sage. This post is about some of my computations. You might want to test them yourself online using the Sage Cell Server.
Basic Definitions
Let \(\mathbb{L}^d=(\mathbb{Z}^d,\mathbb{E}^d)\) be the hypercubic lattice. Let \(p\in[0,1]\). Each edge \(e\in \mathbb{E}^d\) is designated either open with probability \(p\), or closed otherwise, different edges receiving independant states. For \(x,y\in \mathbb{Z}^d\), we write \(x \leftrightarrow y \) if there exists an open path joining \(x\) and \(y\). For \(x\in \mathbb{Z}^d\), we consider the open cluster \(C_x\) containing \(x\) : \[ C_x = \{y \in \mathbb{Z}^d : x \leftrightarrow y \}. \] The percolation probability \(\Theta(p)\) is given by \[ \Theta(p) = P_p(\vert C_0\vert=\infty). \] Finally, the critical probability is defined as \[ p_c = \sup\{p : \Theta(p) = 0 \}. \] The question is to compute \(p_c\). Results in the Chapter give lower bound and upper bound for \(p_c\). Many problems are still open like the one claiming that \(\Theta(p_c) = 0\) for all \(d\geq 2\): it is known only for \(d=2\) and \(d\geq 19\) according to a remark in the chapter.
Some samples when p=0.5
A bond percolation sample inside the box \(\Lambda(m)=[-m,m]^d\) when \(p=0.5\) and \(d=2\):
sage: S = BondPercolationSample(p=0.5, d=2) sage: S.plot(m=40, pointsize=10, thickness=1) Graphics object consisting of 7993 graphics primitives sage: _.show()

Another time gives something different:
sage: S = BondPercolationSample(p=0.5, d=2) sage: S.plot(m=40, pointsize=10, thickness=1) Graphics object consisting of 10176 graphics primitives sage: _.show()

Some samples for ranges of values of p
From p=0.1 to p=0.9:
sage: percolation_graphics_array(srange(0.1,1,0.1), d=2, m=5)

From p=0.41 to p=0.49:
sage: percolation_graphics_array(srange(0.41,0.50,0.01), d=2, m=5)

From p=0.51 to p=0.59:
sage: percolation_graphics_array(srange(0.51,0.60,0.01), d=2, m=5)

Upper bound and lower bound for percolation probability \(\Theta(p)\)
In every case, we have the following upper bound for the percolation probability: \[ \Theta(p) = \mathbb{P}_p(\vert C_0\vert=\infty) \leq \mathbb{P}_p(\vert C_0\vert > 1) = 1 - \mathbb{P}_p(\vert C_0\vert = 1) = 1 - (1-p)^{2d}. \] In particular, if \(p\neq 1\), then \(\Theta(p)<1\). In Sage, define the upper bound:
sage: p,n = var('p,n') sage: d = var('d') sage: upper_bound = 1 - (1-p)^(2*d)
Also, from Equation (3.8), we have the following lower bound: \[ \Theta(p) \geq 1 - \sum_{n=4}^{\infty} n (4(1-p))^n. \]
In Sage, define the lower bound:
sage: p,n = var('p,n') sage: lower_bound = 1 - sum(n*(4*(1-p))^n,n,4,oo) sage: lower_bound.factor() -(3072*p^5 - 14336*p^4 + 26624*p^3 - 24592*p^2 + 11288*p - 2057)/(4*p - 3)^2
This is not defined when \(p=3/4\), but we are interested in the values in the interval \(]3/4,1]\). In particular, for which value of \(p\) is this lower bound strictly larger than zero:
sage: root = lower_bound.find_root(0.76, 0.99); root 0.8639366490304586
Let's now draw a graph of the lower and upper bound:
sage: U = plot(upper_bound(d=2),(0,1),color='red', thickness=3) sage: L = plot(lower_bound,(0.86,1),color='green', thickness=3) sage: G = U + L sage: G += point((root, 0), color='red', size=20) sage: lower = r"$1-\sum_{n=4}^{\infty} n4^n(1-p)^n$" sage: upper = r"$1 -(1-p)^{4}$" sage: title = r"$1-\sum_{n=4}^{\infty} n4^n(1-p)^n\leq\Theta(p)\leq 1 -(1-p)^{2d}$" sage: G += text(title, (.5, 1.05), color='black', fontsize=15) sage: G += text(upper, (.3, 0.5), color='red', fontsize=20) sage: G += text(lower, (.7, 0.5), color='green', fontsize=20) sage: G += text("%.5f"%root,(0.88, .03), color='green', horizontal_alignment='left') sage: G.show()

Thus we conclude that \(\Theta(p) >0\) for \(p>0.8639\) and thus \(p_c \leq 0.8639\).
Percolation probability - dimension 2
The code allows to define the percolation probability function for a given dimension d. It generates n samples and consider the cluster to be infinite if its cardinality is larger than the given stop value.
Here we use Sage adaptative recursion algorithm for drawing the plot of the percolation probability which finds the particular important intervals to ask for more values of the function. See help section of plot function for details. Because T might be long to compute we start with only 4 points.
When stop=100:
sage: T = PercolationProbability(d=2, n=10, stop=100) sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

When stop=1000:
sage: T = PercolationProbability(d=2, n=10, stop=1000) sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

When stop=2000:
sage: T = PercolationProbability(d=2, n=10, stop=2000) sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

Percolation probability - dimension 3
When stop=100:
sage: T = PercolationProbability(d=3, n=10, stop=100) sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

When stop=1000:
sage: T = PercolationProbability(d=3, n=10, stop=1000) sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()
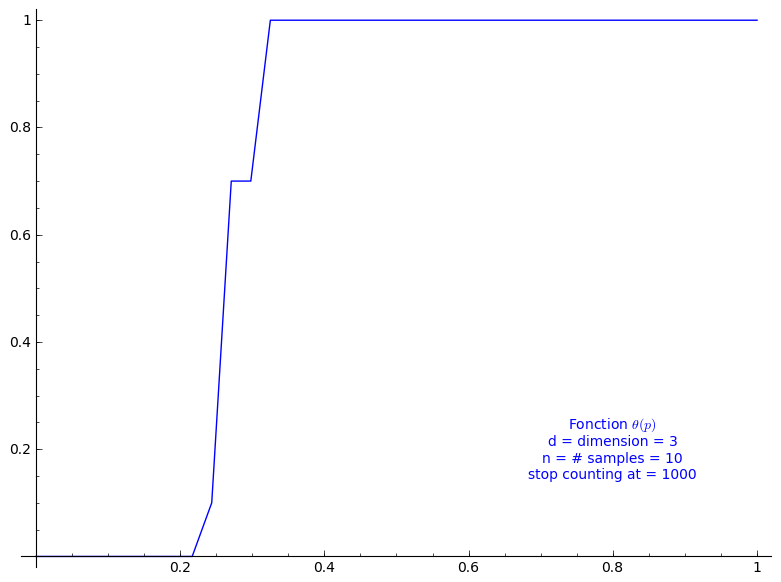
Percolation probability - dimension 4
When stop=100:
sage: T = PercolationProbability(d=4, n=10, stop=100) sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

Percolation probability - dimension 13
When stop=100:
sage: T = PercolationProbability(d=13, n=10, stop=100) sage: T.return_plot((0,1),adaptive_recursion=4,plot_points=4).show()

Theorem 3.2
Theorem 3.2 states that \(0 < p_c < 1\), but its proof does much more in fact. Following the computation we just did for Equation (3.8), we get for \(d=2\) \[ 0.3333 < \frac{1}{2d-1} \leq p_c \leq 0.8639 \] and for \(d=3\): \[ 0.2000 < \frac{1}{2d-1} \leq p_c \leq 0.8639 \] This allows to grasp the improvement brought later by Theorem 3.12.
Connective constant
Using the two following sequences of the On-Line Encyclopedia of Integer Sequences, one can evaluate the connective constant \(\kappa(d)\)
By taking the k-th root of of k-th term of A001411, we may give an approximation of \(\kappa(2)\):
sage: L = [1, 4, 12, 36, 100, 284, 780, 2172, 5916, 16268, 44100, 120292, 324932, 881500, 2374444, 6416596, 17245332, 46466676, 124658732, 335116620, 897697164, 2408806028, 6444560484, 17266613812, 46146397316, 123481354908, 329712786220, 881317491628] sage: for k in range(1, len(L)): print numerical_approx(L[k]^(1/k)) 4.00000000000000 3.46410161513775 3.30192724889463 3.16227766016838 3.09502148400370 3.03400133198980 2.99705187539871 2.96144397263395 2.93714926770637 2.91369345857619 2.89627439045790 2.87949308754677 2.86632078916860 2.85362749495679 2.84328447096562 2.83329615650289 2.82493415671599 2.81684125361654 2.80992368218258 2.80321554383456 2.79738645741910 2.79172363211806 2.78673687369245 2.78188437392354 2.77756387722633 2.77335345579129 2.76956977331575
By taking the k-th root of of k-th term of A001412, we may give an approximation of \(\kappa(3)\):
sage: L = [1, 6, 30, 150, 726, 3534, 16926, 81390, 387966, 1853886, 8809878, 41934150, 198842742, 943974510, 4468911678, 21175146054, 100121875974, 473730252102, 2237723684094, 10576033219614, 49917327838734, 235710090502158, 1111781983442406, 5245988215191414, 24730180885580790, 116618841700433358, 549493796867100942,2589874864863200574, 12198184788179866902, 57466913094951837030, 270569905525454674614] sage: for k in range(1, len(L)): print numerical_approx(L[k]^(1/k)) 6.00000000000000 5.47722557505166 5.31329284591305 5.19079831727404 5.12452137580198 5.06709510955294 5.02933019629493 4.99573287588832 4.97111339009676 4.94876680377358 4.93129192790635 4.91521453865211 4.90209314463520 4.88990167518413 4.87964724632057 4.87004597517131 4.86178722582108 4.85400655861169 4.84719703702142 4.84074902256992 4.83502763526502 4.82958688248615 4.82470487210973 4.82004549244633 4.81582557693112 4.81178552451599 4.80809774735294 4.80455755518719 4.80130435575213 4.79817388859565
Then, \(\kappa(2)\) would be something less than 2.769 and \(\kappa(3)\) would be something less than 4.798.
Theorem 3.12
Thus, we may evaluate the lower bound and upper bound given at Theorem 3.12. For dimension \(d=2\):
sage: k < 2.76956977331575 k < 2.76956977331575 sage: _ / (2.76956977331575 * k) 0.361066909970928 < (1/k) sage: 1 - 0.361066909970928 0.638933090029072
The critical probability of bond percolation on \(\mathbb{L}^d\) with \(d=2\) satisfies \[ 0.3610 < \frac{1}{\kappa(2)} \leq p_c \leq 1 - \frac{1}{\kappa(2)} < 0.6389. \] If we look at the graph of the percolation probability \(\Theta(p)\) we did above for when \(d=2\), it seems that the lower bound is not far from \(p_c\). The lower bound 0.3610 is a small improvement to the simple one got from Theorem 3.2 (0.3333).
Similarly, for dimension \(d=3\):
sage: k < 4.79817388859565 k < 4.79817388859565 sage: _ / (4.79817388859565 * k) 0.208412621805310 < (1/k)
The critical probability of bond percolation on \(\mathbb{L}^d\) with \(d=3\) satisfies \[ 0.2084 < \frac{1}{\kappa(3)} \leq p_c \leq 1 - \frac{1}{\kappa(2)} < 0.6389. \] Again, if we look at the graph of \(\Theta(p)\) we did above for when \(d=3\), it seems that the lower bound 0.2084 is not far from \(p_c\). In this case, the lower bound 0.2084 is a rather small improvement to the lower bound from Theorem 3.2 (0.2000). It might be caused by a poor approximation of \(\kappa(3)\) from the above sequences of only 30 terms from the OEIS.
Some small Sage tricks
14 décembre 2012 | Catégories: sage | View CommentsBelow are some Sage tricks that I gathered from other users of Sage, from sage-devel and other places since one year.
Stop the focus in the Notebook
This Notebook hack of the day was published on sage-devel by William Stein during May 2012 to fix that focus movement in the Notebook:
html('<script>cell_focus=function(x,y){} </script>')
Consult the documentation of a function in the browser
Open the documentation of a particular function in a web browser, from either the command-line or the notebook:
sage: browse_sage_doc(factor)
It works also for methods of an object:
sage: m = matrix(2, range(4)) sage: browse_sage_doc(m.inverse)
I found this command when I consulted the help():
sage: help()
Implicit multiplication
Some behavior in Sage can be made implicit like multiplication and variable definition. This might be good for new users coming from Maple for instance.
Normally, this syntax raises an error:
sage: 34x ------------------------------------------------------------ File "<ipython console>", line 1 34x ^ SyntaxError: invalid syntax
It is possible to make it work:
sage: implicit_multiplication(True) sage: 34x 34*x
Implicit variable definition
The following works only in the Sage Notebook. It allows to turn on automatic definition of variables:
sage: automatic_names(True) sage: x + y + z x + y + z
Turn out automatic show when using plot
Set the default to False for showing plots using any plot commands:
sage: show_default(False)
I prefer False but you may not.
Rerun the patchbot
One can re-run the tests of a particular ticket by adding ?kick to the url of the ticket on the patchbot Sage server. For example, to rerun the tests on the ticket #13461, one can load the following page:
http://patchbot.sagemath.org/ticket/13461/?kick
This trick was shared on sage-devel during August 2012.
Python debugger
The majority of the Best Practices for Scientific Computing are followed by the Sage Development model. But, there is one principle that at least I do not use enough : a debugger. However, a Python debugger exists and a tutorial for using the Python debugger is available on onlamp.com.
I remember that discussion on sage-devel Poll: which debugger do you use? where developers were sharing their debugger tricks. It seems that using print statements is unavoidable.
Computing basic statistics with R
I always knew R is in Sage but never used it even if sometimes I need to compute some statistics of list of numbers. In Sage, one can print statistics of a list of numbers using R:
sage: L = [randint(0,100) for _ in range(20)] sage: r.summary(L) Min. 1st Qu. Median Mean 3rd Qu. Max. 14.00 27.75 57.50 53.45 69.00 98.00
Creation of the number field in \(\sqrt{5}\)
Before learning it from this video of William Stein, I did not know that the square brackets could be used to create such number field:
sage: A = ZZ[sqrt(5)] sage: a,sqrt5 = A.gens() sage: A Order in Number Field in sqrt5 with defining polynomial x^2 - 5 sage: sqrt5 sqrt5
Using Sage locally in the notebook from a server
First, log into the server using the following port setup:
ssh -L 8389:localhoat:8389 [SERVER]
Start the notebook with the given port:
sage -notebook port=8389
This ask for a password, if you forget it, you may reset it by first opening Sage, and by starting the notebook with the option reset=True:
sage: notebook(port=8389, reset=True)
Then, by opening the browser at the following adress, I can log in to the notebook from the server:
http://localhost:8389/home/admin/
Going from Mercurial to Git
Sage will soon move from Mercurial to Git. In the past, I tried to understand the difference between Mercurial and Git. I was never able to find a simple text or blog post on the web explaining in a simple way the differences. One diffence would be about branching. But I was not using branches with Mercurial... As I see it, differences between Mercurial and Git are hard to explain or at least hard to understand.
Anyway, I once found this tutorial on the Git version control system: Understanding Git Conceptually where the approach is "conceptual" and maybe easier for the mathematician. For instance, in Section 1 it is written that repositories can be "visualized as a directed acyclic graph of commit objects". I still haven't go through this tutorial but I consider to start with this one.
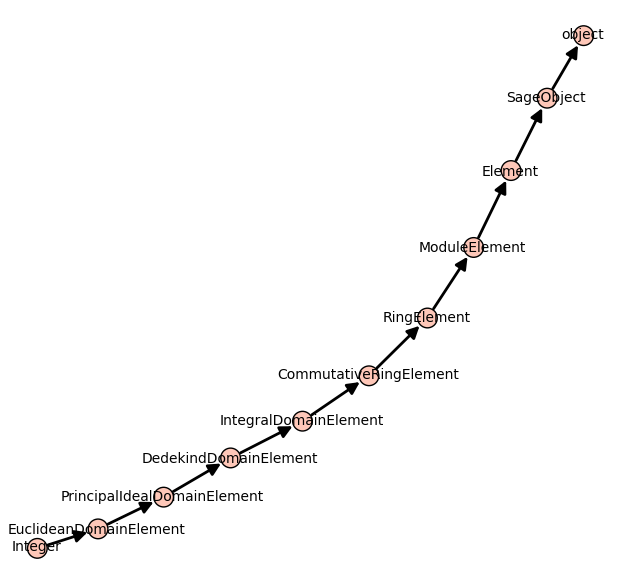
Inheritance tree
One may draw the inheritance tree of a class with the following command:
sage: class_graph(Integer).plot()
Using Sage + graphviz + dot2tex + tikz + tikz2pdf to draw a graph
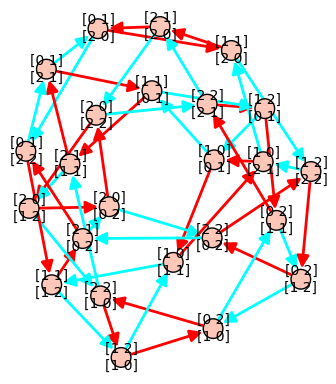
13 novembre 2012 | Mise à jour: 16 novembre 2012 | Catégories: latex, sage | View CommentsLet's first construct a graph that we will use in our examples below. We first construct a finite group generated by 2 by 2 matrices on the field \(GF(3)\). The group contains 24 elements. We then construct its Cayley graph:
sage: F = GF(3) sage: gens = [matrix(F,2,[1,0, 1,1]), matrix(F,2, [1,1, 0,1])] sage: group = MatrixGroup(gens); group Matrix group over Finite Field of size 3 with 2 generators: [[[1, 0], [1, 1]], [[1, 1], [0, 1]]] sage: group.cardinality() 24 sage: G = group.cayley_graph()
Default graph plot
The default graph plot in Sage is:
sage: G.show(color_by_label=True)
Using view is actually broken when vertices are matrices because default format (format='tkz_graph') does not support it:
sage: view(G) An error occurred. ... LaTex error
Installing dot2tex + graphviz
One may get another kind of tikz output using the dot2tex.spkg together with graphviz. To know what is the latest available version of dot2tex use the command optional_packages():
sage: [x for x in flatten(optional_packages()) if 'dot2tex' in x] ['dot2tex-2.8.7-2']
The command to install the most recent version of dot2tex.spkg do from the command line (where you replace the version numbers by the above output):
sage -i dot2tex-2.8.7-2
As the documentation of G.layout_graphviz() says, install graphviz >= 2.14 so that the programs dot, neato, ... are in your path. The graphviz suite can be download from the graphviz website.
Basic Usage
This should allow the following to work:
sage: G.set_latex_options(format='dot2tex', prog='neato') sage: G.set_latex_options(color_by_label=True) sage: view(G)
Limits of the basic usage
With the above usage, you will find that the command view(G) command is very slow and that sometimes it just doesn't work and gives a Latex error like this:
sage: G.set_latex_options(format='dot2tex', prog='dot') sage: view(G) An error occurred. ... LaTex error
This is because the default compilation is just unappropriate for our usage (I still wonder for which usage it can be appropriate). In fact, the default compilation is first trying the conversion tex to dvi to png using latex and dvipng. If the dvipng part does not work for whatever reason (which is our case), it will then try the conversion dvi to ps to pdf using dvips and ps2pdf. This worked above for prog='neato' but not for prog='dot' because dvipng does not seem to like when latex produces Overfull \hbox and Overfull \vbox.
The Best Usage
The compilation strategy can be changed by using the engine option and by setting it to 'pdflatex'. Also the Overfull problem can be solved using the option tightpage=True:
sage: G.set_latex_options(format='dot2tex', prog='dot') sage: G.set_latex_options(color_by_label=True) sage: view(G, engine='pdflatex', tightpage=True)
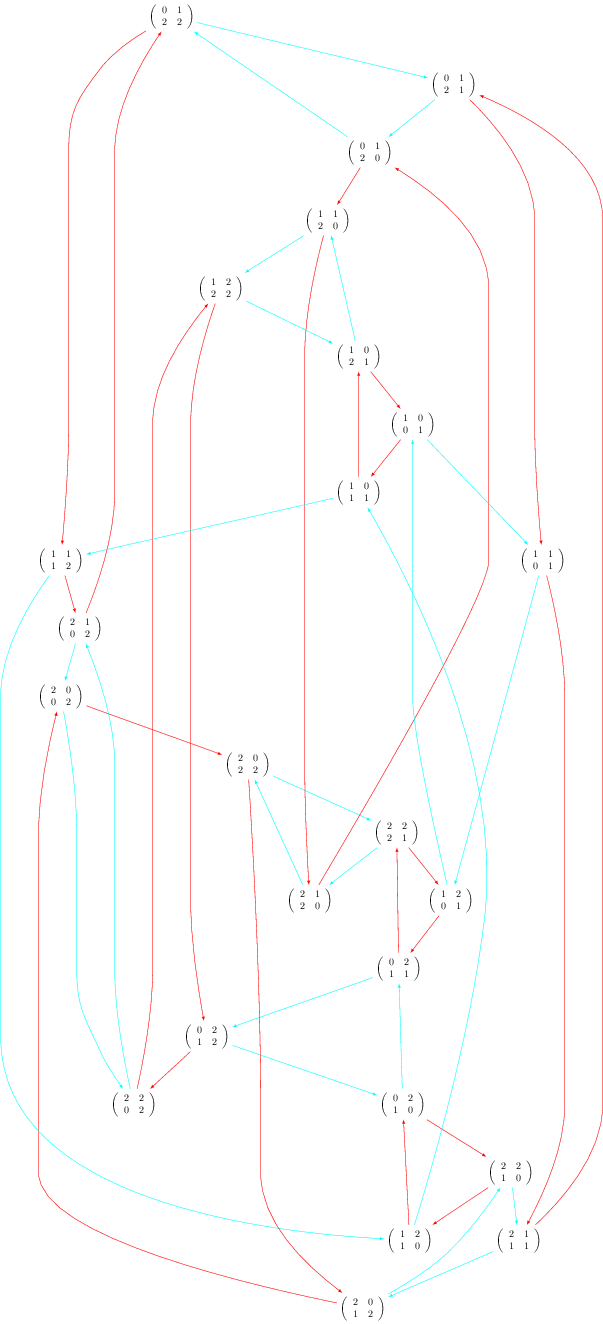
More options
The variable prog is for the program used for the layout. It must be a string corresponding to one of the software of the graphviz suite. Accepted values for prog are:
- 'dot' (the default)
- 'neato'
- 'twopi'
- 'circo'
- 'fdp'
When using format='dot2tex', other available options are:
sage: G.set_latex_options(color_by_label=True) sage: G.set_latex_options(edge_labels=True) sage: G.set_latex_options(edge_colors=I_dont_know_what)
Consult the help for more details:
sage: opts = G.latex_options() sage: opts.set_option?
However, these other options do not seem to work perfectly. I don't know what format to give to edges_colors and edge_labels=True seems broken. I posted a workaround on the sagetrac to fix it.
Using the tikz2pdf script instead of the command view
Alternatively, when I get problems with the view command, I use my script tikz2pdf instead:
sage: G.set_latex_options(format='dot2tex', prog='dot') sage: G.set_latex_options(color_by_label=True) sage: G.latex_options() LaTeX options for Digraph on 24 vertices: {'prog': 'dot', 'color_by_label': True, 'format': 'dot2tex'} sage: s = G.latex_options().dot2tex_picture() sage: f = open('graph_dot.tikz', 'w') sage: f.write(s) sage: f.close() sage: !tikz2pdf graph_dot.tikz Using template ... tikz2pdf: calling pdflatex... tikz2pdf: Output written to 'graph_dot.pdf'.
Draw a graph of matrices in LaTeX using Sage
18 octobre 2012 | Catégories: latex, sage | View CommentsIn version 5.3 of Sage, if the vertices of a graph are matrices, then the default latex output does not compile. The default format is a tikzpicture and uses the tkz-berge library. One solution is to change the format to dot2tex. See below.
The default tikz output is:
sage: m = matrix(3, range(9)) sage: m.set_immutable() sage: G = Graph() sage: G.add_vertex(m) sage: latex(G) \begin{tikzpicture} % \useasboundingbox (0,0) rectangle (5.0cm,5.0cm); % \definecolor{cv0}{rgb}{0.0,0.0,0.0} \definecolor{cfv0}{rgb}{1.0,1.0,1.0} \definecolor{clv0}{rgb}{0.0,0.0,0.0} % \Vertex[style={minimum size=1.0cm,draw=cv0,fill=cfv0,text=clv0,shape=circle}, LabelOut=false,L=\hbox{$\left(\begin{array}{rrr} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{array}\right)$},x=2.5cm,y=2.5cm]{v0} % % \end{tikzpicture}
This output does not compile. Here is the error I get:
sage: view(G)
An error occurred.
This is pdfTeX, Version 3.1415926-1.40.10 (TeX Live 2009) (format=pdflatex 2011.4.19) 18 OCT
2012 21:34
entering extended mode
[...]
! Use of \tikz@@scope@env doesn't match its definition.
\pgfutil@ifnextchar #1#2#3->\let \pgfutil@reserved@d =#1\def \pgfutil@reserved@a {
#2}\def \pgf
util@reserved@b {#3}\futurelet \pgfutil@let@token \pgfutil@ifnch
l.54 \end{array}\right)$},x=2.5cm,y=2.5cm]{v0}
If you say, e.g., `\def\a1{...}', then you must always
put `1' after `\a', since control sequence names are
made up of letters only. The macro here has not been
followed by the required stuff, so I'm ignoring it.
! Use of \tikz@@scope@env doesn't match its definition.
[...]
! ==> Fatal error occurred, no output PDF file produced!
Latex error
The command to install dot2tex:
sage -i dot2tex-2.8.7-2
As the documentation of G.layout_graphviz() says, install graphviz >= 2.14 so that the programs dot, neato, ... are in your path. This allows the following to work:
sage: m = matrix(3, range(9)) sage: m.set_immutable() sage: G = Graph() sage: G.add_vertex(m) sage: G.set_latex_options(format='dot2tex') sage: view(G)
To obtain the tikz code:
sage: tikz_string = G.latex_options().dot2tex_picture() sage: print tikz_string \begin{tikzpicture}[>=latex,line join=bevel,] %% \node (012345678) at (34bp,22bp) [draw,draw=none] {$\left(\begin{array}{rrr}0 & 1 & 2 \\3 & 4 & 5 \\6 & 7 & 8\end{array}\right)$}; % \end{tikzpicture}
Définition d'une série formelle en Sage
25 septembre 2012 | Catégories: sage | View CommentsQuestion :
Comment fait-on en sage pour avoir le terme général d'une serie formelle en \(x\) comme \(1/(1-q^2x)\) par exemple, où \(q\) est un paramètre (il faudrait obtenir \(q^{2k} x^k\) ) ?
Quelques exemples se trouvent dans la documentation sur les espèces en Sage, mais il faut faire quand même quelques essais et combiner quelques idées pour y parvenir. Une façon de procéder est définir une espèce récursive en assignant un poids pour le paramètre (voir Weighted Species).
Sous une forme récursive, la série s'écrit :
\[ L = 1 + q^2 \cdot x \cdot L \]
Alors, en sage, on écrira:
sage: q = QQ['q'].gen() sage: E = species.EmptySetSpecies() sage: X = species.SingletonSpecies(weight=q^2) sage: L = CombinatorialSpecies() sage: L.define(E+X*L) sage: L.generating_series().coefficients(10) [1, q^2, q^4, q^6, q^8, q^10, q^12, q^14, q^16, q^18]
Aussi:
sage: X.generating_series().coefficients(5) [0, q^2, 0, 0, 0] sage: E.generating_series().coefficients(5) [1, 0, 0, 0, 0]
On peut faire le produit de deux espèces:
sage: A = X * X sage: A.generating_series().coefficients(5) [0, 0, q^4, 0, 0]
On peut faire la somme de deux espèces:
sage: B = X + X sage: B.generating_series().coefficients(5) [0, 2*q^2, 0, 0, 0]
mais pas la différence:
sage: E - X Traceback (most recent call last) : ... TypeError: unsupported operand type(s) for -: 'EmptySetSpecies_class' and 'SingletonSpecies_class'
ni le quotient:
sage: E / X Traceback (most recent call last): ... TypeError: unsupported operand type(s) for /: 'EmptySetSpecies_class' and 'SingletonSpecies_class'
Encore moins une combinaison des deux:
sage: E/(E-X) Traceback (most recent call last) : ... TypeError: unsupported operand type(s) for -: 'EmptySetSpecies_class' and 'SingletonSpecies_class'
et je ne sais pas pourquoi...
« Previous Page -- Next Page »
