My status report at Sage Days 57 (RecursivelyEnumeratedSet)
11 avril 2014 | Catégories: sage | View CommentsAt Sage Days 57, I worked on the trac ticket #6637: standardize the interface to TransitiveIdeal and friends. My patch proposes to replace TransitiveIdeal and SearchForest by a new class called RecursivelyEnumeratedSet that would handle every case.
A set S is called recursively enumerable if there is an algorithm that enumerates the members of S. We consider here the recursively enumerated set that are described by some seeds and a successor function succ. The successor function may have some structure (symmetric, graded, forest) or not. Many kinds of iterators are provided: depth first search, breadth first search or elements of given depth.
TransitiveIdeal and TransitiveIdealGraded
Consider the permutations of \(\{1,2,3\}\) and the poset generated by the method permutohedron_succ:
sage: P = Permutations(3)
sage: d = {p:p.permutohedron_succ() for p in P}
sage: S = Poset(d)
sage: S.plot()
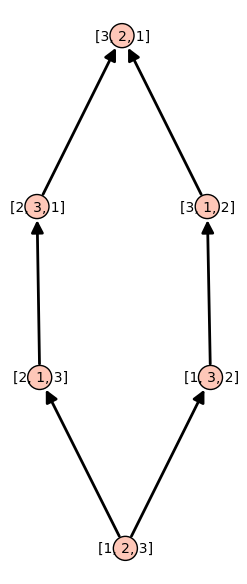
The TransitiveIdeal allows to generates all permutations from the identity permutation using the method permutohedron_succ as successor function:
sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1,2,3])]
sage: T = TransitiveIdeal(succ, seed)
sage: list(T)
[[1, 2, 3], [2, 1, 3], [1, 3, 2], [2, 3, 1], [3, 2, 1], [3, 1, 2]]
Remark that the previous ordering is neither breadth first neither depth first. It is a naive search because it stores the element to process in a set instead of a queue or a stack.
Note that the method permutohedron_succ produces a graded poset. Therefore, one may use the TransitiveIdealGraded class instead:
sage: T = TransitiveIdealGraded(succ, seed) sage: list(T) [[1, 2, 3], [2, 1, 3], [1, 3, 2], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
For TransitiveIdealGraded, the enumeration is breadth first search. Althougth, if you look at the code (version Sage 6.1.1 or earlier), we see that this iterator do not make use of the graded hypothesis at all because the known set remembers every generated elements:
current_level = self._generators known = set(current_level) depth = 0 while len(current_level) > 0 and depth <= self._max_depth: next_level = set() for x in current_level: yield x for y in self._succ(x): if y == None or y in known: continue next_level.add(y) known.add(y) current_level = next_level depth += 1 return
Timings for TransitiveIdeal
sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1..5])]
sage: T = TransitiveIdeal(succ, seed)
sage: %time L = list(T)
CPU times: user 26.6 ms, sys: 1.57 ms, total: 28.2 ms
Wall time: 28.5 ms
sage: seed = [Permutation([1..8])] sage: T = TransitiveIdeal(succ, seed) sage: %time L = list(T) CPU times: user 14.4 s, sys: 141 ms, total: 14.5 s Wall time: 14.8 s
Timings for TransitiveIdealGraded
sage: seed = [Permutation([1..5])] sage: T = TransitiveIdealGraded(succ, seed) sage: %time L = list(T) CPU times: user 25.3 ms, sys: 1.04 ms, total: 26.4 ms Wall time: 27.4 ms
sage: seed = [Permutation([1..8])] sage: T = TransitiveIdealGraded(succ, seed) sage: %time L = list(T) CPU times: user 14.5 s, sys: 85.8 ms, total: 14.5 s Wall time: 14.7 s
In conlusion, use TransitiveIdeal for naive search algorithm and use TransitiveIdealGraded for breadth search algorithm. Both class do not use the graded hypothesis.
Recursively enumerated set with a graded structure
The new class RecursivelyEnumeratedSet provides all iterators for each case. The example below are for the graded case.
Depth first search iterator:
sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1..5])]
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='graded')
sage: it_depth = R.depth_first_search_iterator()
sage: [next(it_depth) for _ in range(5)]
[[1, 2, 3, 4, 5],
[1, 2, 3, 5, 4],
[1, 2, 5, 3, 4],
[1, 2, 5, 4, 3],
[1, 5, 2, 4, 3]]
Breadth first search iterator:
sage: it_breadth = R.breadth_first_search_iterator() sage: [next(it_breadth) for _ in range(5)] [[1, 2, 3, 4, 5], [1, 3, 2, 4, 5], [1, 2, 4, 3, 5], [2, 1, 3, 4, 5], [1, 2, 3, 5, 4]]
Elements of given depth iterator:
sage: list(R.elements_of_depth_iterator(9)) [[5, 4, 2, 3, 1], [4, 5, 3, 2, 1], [5, 3, 4, 2, 1], [5, 4, 3, 1, 2]] sage: list(R.elements_of_depth_iterator(10)) [[5, 4, 3, 2, 1]]
Levels (a level is a set of elements of the same depth):
sage: R.level(0)
[[1, 2, 3, 4, 5]]
sage: R.level(1)
{[1, 2, 3, 5, 4], [1, 2, 4, 3, 5], [1, 3, 2, 4, 5], [2, 1, 3, 4, 5]}
sage: R.level(2)
{[1, 2, 4, 5, 3],
[1, 2, 5, 3, 4],
[1, 3, 2, 5, 4],
[1, 3, 4, 2, 5],
[1, 4, 2, 3, 5],
[2, 1, 3, 5, 4],
[2, 1, 4, 3, 5],
[2, 3, 1, 4, 5],
[3, 1, 2, 4, 5]}
sage: R.level(3)
{[1, 2, 5, 4, 3],
[1, 3, 4, 5, 2],
[1, 3, 5, 2, 4],
[1, 4, 2, 5, 3],
[1, 4, 3, 2, 5],
[1, 5, 2, 3, 4],
[2, 1, 4, 5, 3],
[2, 1, 5, 3, 4],
[2, 3, 1, 5, 4],
[2, 3, 4, 1, 5],
[2, 4, 1, 3, 5],
[3, 1, 2, 5, 4],
[3, 1, 4, 2, 5],
[3, 2, 1, 4, 5],
[4, 1, 2, 3, 5]}
sage: R.level(9)
{[4, 5, 3, 2, 1], [5, 3, 4, 2, 1], [5, 4, 2, 3, 1], [5, 4, 3, 1, 2]}
sage: R.level(10)
{[5, 4, 3, 2, 1]}
Recursively enumerated set with a symmetric structure
We construct a recursively enumerated set with symmetric structure and depth first search for default enumeration algorithm:
sage: succ = lambda a: [(a[0]-1,a[1]), (a[0],a[1]-1), (a[0]+1,a[1]), (a[0],a[1]+1)] sage: seeds = [(0,0)] sage: C = RecursivelyEnumeratedSet(seeds, succ, structure='symmetric', algorithm='depth') sage: C A recursively enumerated set with a symmetric structure (depth first search)
In this case, depth first search is the default algorithm for iteration:
sage: it_depth = iter(C) sage: [next(it_depth) for _ in range(10)] [(0, 0), (0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8), (0, 9)]
Breadth first search. This algorithm makes use of the symmetric structure and remembers only the last two levels:
sage: it_breadth = C.breadth_first_search_iterator() sage: [next(it_breadth) for _ in range(10)] [(0, 0), (0, 1), (0, -1), (1, 0), (-1, 0), (-1, 1), (-2, 0), (0, 2), (2, 0), (-1, -1)]
Levels (elements of given depth):
sage: sorted(C.level(0)) [(0, 0)] sage: sorted(C.level(1)) [(-1, 0), (0, -1), (0, 1), (1, 0)] sage: sorted(C.level(2)) [(-2, 0), (-1, -1), (-1, 1), (0, -2), (0, 2), (1, -1), (1, 1), (2, 0)]
Timings for RecursivelyEnumeratedSet
We get same timings as for TransitiveIdeal but it uses less memory so it might be able to enumerate bigger sets:
sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1..5])]
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='graded')
sage: %time L = list(R)
CPU times: user 24.7 ms, sys: 1.33 ms, total: 26.1 ms
Wall time: 26.4 ms
sage: seed = [Permutation([1..8])] sage: R = RecursivelyEnumeratedSet(seed, succ, structure='graded') sage: %time L = list(R) CPU times: user 14.5 s, sys: 70.2 ms, total: 14.5 s Wall time: 14.6 s
Demo of the IPython notebook at Sage Paris group meeting
06 mars 2014 | Catégories: ipython, sage | View CommentsToday I am presenting the IPython notebook at the meeting of the Sage Paris group. This post gathers what I prepared.
Installation
First you can install the ipython notebook in Sage as explained in this previous blog post. If everything works, then you run:
sage -ipython notebook
and this will open a browser.
Turn on Sage preparsing
Create a new notebook and type:
In [1]: 3 + 3 6 In [2]: 2 / 3 0 In [3]: matrix Traceback (most recent call last): ... NameError: name 'matrix' is not defined
By default, Sage preparsing is turn off and Sage commands are not known. To turn on the Sage preparsing (thanks to a post of Jason on sage-devel):
%load_ext sage.misc.sage_extension
Since sage-6.2, according to sage-devel, the command is:
%load_ext sage
You now get Sage commands working in ipython:
In [4]: 3 + 4 Out[4]: 7 In [5]: 2 / 3 Out[5]: 2/3 In [6]: type(_) Out[6]: <type 'sage.rings.rational.Rational'> In [7]: matrix(3, range(9)) Out[7]: [0 1 2] [3 4 5] [6 7 8]
Scroll and hide output
If the output is too big, click on Out to scroll or hide the output:
In [8]: range(1000)
Sage 3d Graphics
3D graphics works but open in a new Jmol window:
In [9]: sphere()
Sage 2d Graphics
Similarly, 2D graphics works but open in a new window:
In [10]: plot(sin(x), (x,0,10))
Inline Matplotlib graphics
To create inline matplotlib graphics, the notebook must be started with this command:
sage -ipython notebook --pylab=inline
Then, a matplotlib plot can be drawn inline (example taken from this notebook):
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 3*np.pi, 500)
plt.plot(x, np.sin(x**2))
plt.title('A simple chirp');
Or with:
%load http://matplotlib.org/mpl_examples/showcase/integral_demo.py
According to the previous cited notebook, it seems, that the inline mode can also be decided from the notebook using a magic command, but with my version of ipython (0.13.2), I get an error:
In [11]: %matplotlib inline ERROR: Line magic function `%matplotlib` not found.
Use latex in a markdown cell
Change an input cell into a markdown cell and then you may use latex:
Test $\alpha+\beta+\gamma$
Output in latex
The output can be shown with latex and mathjax using the ipython display function:
from IPython.display import display, Math def my_show(obj): return display(Math(latex(obj))) y = 1 / (x^2+1) my_show(y)
ipynb format
Create a new notebook with only one cell. Name it range_10 and save:
In [1]: range(10) Out[1]: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
The file range_10.ipynb is saved in the directory. You can also download it from File > Download as > IPython (.ipynb). Here is the content of the file range_10.ipynb:
{
"metadata": {
"name": "range_10"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": false,
"input": [
"range(10)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 1,
"text": [
"[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]"
]
}
],
"prompt_number": 1
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
}
ipynb is just json
A ipynb file is written in json format. Below, we use json to open the file `range_10.ipynb as a Python dictionnary.
sage: s = open('range_10.ipynb','r').read()
sage: import json
sage: D = json.loads(s)
sage: type(D)
dict
sage: D.keys()
[u'nbformat', u'nbformat_minor', u'worksheets', u'metadata']
sage: D
{u'metadata': {u'name': u'range_10'},
u'nbformat': 3,
u'nbformat_minor': 0,
u'worksheets': [{u'cells': [{u'cell_type': u'code',
u'collapsed': False,
u'input': [u'range(10)'],
u'language': u'python',
u'metadata': {},
u'outputs': [{u'output_type': u'pyout',
u'prompt_number': 1,
u'text': [u'[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]']}],
u'prompt_number': 1},
{u'cell_type': u'code',
u'collapsed': False,
u'input': [],
u'language': u'python',
u'metadata': {},
u'outputs': []}],
u'metadata': {}}]}
Load vaucanson.ipynb
Download the file vaucanson.ipynb from the last meeting of Paris Sage Users. You can view the complete demo including pictures of automaton even if you are not able to install vaucanson on your machine.
IPython notebook from a Python file
In a Python file, separate your code with the following line to create cells:
# <codecell>
For example, create the following Python file. Then, import it in the notebook. It will get translated to ipynb format automatically.
# -*- coding: utf-8 -*- # <nbformat>3.0</nbformat> # <codecell> %load_ext sage.misc.sage_extension # <codecell> matrix(4, range(16)) # <codecell> factor(2^40-1)
More conversion
Since release 1.0 of IPython, many conversion from ipynb to other format are possible (html, latex, slides, markdown, rst, python). Unfortunately, the version of IPython in Sage is still 0.13.2 as of today but the version 1.2.1 will be in sage-6.2.
Ranking algorithms for competitive Ultimate
02 mars 2014 | Mise à jour: 26 mars 2014 | Catégories: ultimate | View CommentsRanking teams is a great question. There can be a lot of mathematics and complicated computations involved. The ranking algorithm used by USAUltimate is not an exception. Taking as huge input the results of thousands of games played during a season, it outputs a ranking of teams. Recently, USA Ultimate annonced modifications to their ranking algorithm for the 2014 Season which I see as local changes keeping the same global approach. I quickly shared my thoughts on ultiworld recently. Then, I was asked to explain my ideas more deeply which I do in this text.
I believe the actual USA ranking algorithm is not too bad at fullfilling its objective: decide bids per region. Once the number of bids are set, the season results and the USA ranking has no impact anymore on deciding which team is the best. The best team will be the team who wons the nationals after qualifying through sectionals and regionals. But depending on the objective to achieve, the choice of ranking algorithm can be more important as its role is more determinant:
Role A. Rank the teams at all time of the year (like tennis ATP and WTA rankings)Role B. Choose the Season Champion (like in Formula 1)Role C. Select teams for a Championship (Quebec Ultimate 4 on 4 Circuit)Role D. Decide bids per region (USAU)
Depending on the role of the ranking, the chosen ranking algorithm might be more or less suited. In this text, I explain my point of view on ranking algorithms for competitive Ultimate. I consider the case where the season is made of many tournaments and where the ranking has a role in deciding the national champion, that is like role B or C above. It may also apply for deciding bids per region (role D). But whatever its role, to me, a good ranking algorithm for competitive Ultimate must:
- Produce a ranking
- Consider the structure of tournaments (not every game worth the same)
- Be predictable
- Reward what is the most valuable (winning when it counts)
Below, I explain each of the above condition. I also propose a ranking algorithm for competitive ultimate based on results of tournaments. This text ends with an example on 2013 Club Open season to see how my proposed ranking would work for bid allocation in USA Ultimate. In general, I hope my text can stimulate a reflexion about what algorithm is best suited for competitive ultimate.
1. Produce a ranking
Of course, the ranking algorithm should produce a overall ranking of teams. Everybody agrees with this.
2. Consider the structure of tournaments (not every game worth the same)
To me the principal weekness of the actual USAU Ranking algorithm is that it doesn't see the structure of tournaments. The algorithm can be great for a league or whatever sport where games are worth the same but not for competitive Ultimate where games are played during tournaments. For the algorithm used by USAU, a tournament is just a bunch of random games. The algorithm does not see the difference between the saturday morning game and the sunday afternoon final (apart the one day difference which won't affect much).
The following paradox illustrates how the results of games in a tournament is completely independent of the outcome of the tournament itself. Four teams (A, B, C and D) play in a tournament. The format is a round robin followed by semi-finals, final and 3rd place game: 10 games all in all. The results are (in no particular order):
- game #0: (15) A - C (7)
- game #1: (15) B - D (6)
- game #2: (15) A - D (8)
- game #3: (15) B - C (10)
- game #4: (15) A - B (12)
- game #5: (15) C - D (9)
- game #6: (12) A - D (15)
- game #7: (7) B - C (15)
- game #8: (8) A - B (15)
- game #9: (9) C - D (15)
From this information only, can you decide which team won the tournament? The answer is NO. If games #0, #1, #2, #3, #4, #5 are pool play games, then the seeding out of pool play is A(3-0), B(2-1), C(1-2), D(0-3). Games #6 and #7 are the semis, game #8 is the 3rd place game and game #9 is the final. Team D win the tournament. Final standing is D-C-B-A.
If games #0,#1,#6,#7,#8,#9 are played in the pool, then the pool outcome becomes B(2-1), D(2-1), A(1-2), C(1-2). Team B and C play in semi final game #3 while Team A and D play their semi in game #2. The final game is game #4. The 3rd place is game #5. Team A win the tournament. Final standing is A-B-C-D.
After the tournament, we can discuss about what should be the proper ranking of those four teams based on the results of the 10 games they played. But, there are good chances that we are just wrong as the above paradox shows. In a tournament all games are not equal. It is all about the context. A good ranking algorithm should consider the format of tournaments and accept that some games worth more than others. How to do this? The actual algorithm is already very complicated. How to put more value to particular games? Maybe possible, but may be complicated as well.
I believe there is an easy solution to this. The algorithm must take a step back. Looking at games is like looking at the microscope: we don't see the global picture. Which team get the trophy at the end of the tournament in front of everyone without contestation from anybody? The trophy is given at the end of the tournament to the team who reached the final and won it. This is the best team. The best team is not the one who got the best overall game results. This is why I believe ranking algorithm in competitive Ultimate should be based on the outcome of tournaments and not on the outcome of games.
3. Be predictable
In a text by Lou Burruss about ranking published during 2012, the author speak about the recursive aspect of the actual ranking algorithm making it unpredictable:
"In conversation with Sholom, he made clear there is still some mystery to this very complex process. Even after 20 years of official rankings and simulations, it is impossible to predict exactly how things will behave."
On the contrary, if the ranking system is predictable, then teams know in advance that winning a certain game will give them exactly 200 pts, let's say, and this is the amount they need to become #1 in the country, then it will be one more motivation to win the game.
This is when ranking is not anymore only about ranking. Ranking can also be a source of motivation for team to improve. But ranking will do this at its best when it is predictable. This is why I believe USA Ultimate should look into this if they want to enhance the level of competition as they claim:
"In the ongoing effort to enhance the level of competition and achieve organizational goals, USA Ultimate continues to look to improve the ranking algorithm [...]."
4. Reward what is the most valuable (winning when it counts)
In my opinion, ranking should reward what is the most valuable by the community. This should correspond to what is the most difficult to achieve. Again, this point is a necessary condition for the ranking to be used as a source of motivation for team to improve.
If a ranking values something else, then people won't value the ranking and team won't try to improve themselve to get a better ranking. For example, think about a ranking that would only consider the best differential. We all know that the best differential in a tournament can be reached by the team G who finishes 7th out of 16 teams. The team G will think they are the best in the country and they won't try to win a tournament : too much effort and useless. The team A who put all the effort to get to the final and win it will wonder if they are optimizing the good thing. They will be less motivated to win another tournament.
Naturally, the community values teams getting in the final and winning it. This is what I call the natural attractor. The ranking algorithm chosen also defines a ranking attractor. As we have seen in the last paragraph, the two attractors can be different. But, I strongly believe the best choice of ranking algorithm is when syzygy (picture here) happens, that is when the ranking attractor equals the natural attractor.
"The syzygy produces the more powerful spring tide due to the enhanced gravitational effect of the Sun added to the Moon's gravitational pull."
In this situation, the natural attractors and the ranking attractor double their forces and team then really wants to win tournaments because they get the natural recognition from the community plus they get an high rank in the official ranking. This is the best way to optimize the improvement of teams.
It is known that the actual ranking algorithm encourages teams to play a bit differently than they would if it was just about winning tournaments. In Maximizing Your Team’s Ranking: Strength of Schedule or Margin of Victory? (Dec. 2013), Scott Schriner confirms this. He wrote:
"To increase your game performance score, you will want to win more games — but also win each game by as large of a margin as possible. This might include playing your starters longer than necessary, or loading up your D Line with an O Line handler even if you don’t need that break. Of course that decision carries with it other tradeoffs: you may increase injury risk or stall the development of younger players on your team."
I believe it is a mark of respect for tournament structure that the ranking attractor correspond to the the natural attractor. Moreover, this system is trusting teams and let them all the liberty they need to win a tournament. Good team will peak at the good moment and will try new strategies or give more playing time to rookies at other moment. Teams that try to optimize every point at every game do not improve and do not push the game further.
A ranking system for competitive Ultimate
There is a important observation to be made when creating overall ranking in competitive ultimate. The output of a tournament is a ranking of teams. Why not build on this to create overall ranking? A natural system is to give points to teams according to the final ranking. In such a system, teams needs to win tournaments to get the maximal amount of points.
I think a system like tennis ATP and WTA ranking is a good inspiration for competitive ultimate. Tennis players go to tournaments they choose. Some tournaments worth more (Grand Slam) some less (ATP World Tour Masters 1000, ATP 500, ATP 250). The number of points of a tennis player is the sum of its best 18 results.
The problem with tennis compared to Ultimate is that there are no placement games. The outcome of a tennis tournament is that you either win the final, made the final, made the semis, made the quarters, made the round of 16, and so on. In Ultimate, there are placement games and finishing 9th is better than finishing 16th. Also, 18 tournaments is a lot. We need to consider less tournaments.
Since 2007, in Quebec we adapted the ATP ranking to Ultimate tournaments with placement games. In 2011, the series became so popular. We needed to adjust the system (88 teams took part in the Mars Attaque 2011 but only 32 got points). Since 2011, 1000 pts is given to the winner of a Grand Slam event, 938 pts is given to the finalist, 884 pts is given to the 3rd place, 835 pts to the 4th place and this goes until the team finishing in 50th place who obtain 1pt. The number of points is obtained from the integral of a logarithmic function. I am going to write another text on my blog where I explain the details and the math behind the system.
Example : ranking of USA Open Club team during 2013 regular season
As an example I am considering the 2013 USA Club Open seaon. I selected the following list of 14 tournaments. Those tournaments are divided into 2 groups (7 tournaments of 500 points, 7 elite tournaments of 1000 points).
| Tournaments considered | Points for champion |
| Cal State | 500 |
| Cazenovia | 500 |
| No Surf | 500 |
| Old Dominion Q. | 500 |
| Mot. Throwdown | 500 |
| San Diego Slammer | 500 |
| Col. Cup noTCT | 500 |
| Chesapeake Invite | 1000 |
| Club Terminus | 1000 |
| Colorado Cup | 1000 |
| Heavyweights | 1000 |
| Pro Flight Finale | 1000 |
| US Open | 1000 |
| West Coast Cup | 1000 |
Below is the resulting ranking made from the 2013 USA Club Open season with the parameters chosen above. Comments are welcome.
Pos Pts Team name Rg Best 2nd best 3rd best +-----+------+-----------------------------+----+----------------------------+----------------------------+----------------------------+ 1 2746 Doublewide SC 1 (1000) Colorado Cup 2 (911) Pro Flight Finale 3 (835) US Open 2 2670 PoNY NE 1 (1000) Club Terminus 3 (835) Colorado Cup 3 (835) Chesapeake Invite 3 2619 Revolver SW 1 (1000) US Open 2 (911) West Coast Cup 5 (708) Pro Flight Finale 4 2603 Sockeye NW 1 (1000) West Coast Cup 3 (835) Club Terminus 4 (768) Pro Flight Finale 5 2603 Machine GL 1 (1000) Heavyweights 3 (835) Pro Flight Finale 4 (768) Club Terminus 6 2387 Johnny Bravo SC 2 (911) Colorado Cup 4 (768) West Coast Cup 5 (708) Club Terminus 7 2377 Ironside NE 2 (911) US Open 2 (911) Chesapeake Invite 8 (555) Pro Flight Finale 8 2361 GOAT NE 1 (1000) Pro Flight Finale 5 (708) Chesapeake Invite 6 (653) Club Terminus 9 2166 Chain Lightning SE 2 (911) Club Terminus 6 (653) Chesapeake Invite 7 (602) Pro Flight Finale 10 2140 Sub Zero NC 1 (1000) Chesapeake Invite 5 (708) Heavyweights 11 (432) Club Terminus 11 2043 Ring of Fire SE 3 (835) US Open 6 (653) Pro Flight Finale 8 (555) Chesapeake Invite 12 1937 High Five GL 3 (835) Heavyweights 7 (602) Chesapeake Invite 1 (500) No Surf 13 1927 Rhino NW 5 (708) Colorado Cup 5 (708) West Coast Cup 9 (511) Club Terminus 14 1910 Madison Club NC 2 (911) Heavyweights 7 (602) Colorado Cup 12 (397) Club Terminus 15 1881 Truck Stop MA 4 (768) Colorado Cup 7 (602) Club Terminus 9 (511) Chesapeake Invite 16 1685 Inception SC 4 (768) Heavyweights 1 (500) Col. Cup noTCT 3 (417) San Diego Slammer 17 1492 Streetgang SW 6 (653) Heavyweights 2 (455) San Diego Slammer 4 (384) Cal State 18 1455 Chicago Club GL 5 (708) US Open 4 (384) Mot. Throwdown 13 (363) Heavyweights 19 1340 LA Renegade SW 7 (602) Heavyweights 4 (384) Cal State 5 (354) San Diego Slammer 20 1302 Condors SW 1 (500) Cal State 1 (500) San Diego Slammer 15 (302) Colorado Cup 21 1284 Madcow GL 2 (455) Mot. Throwdown 11 (432) Colorado Cup 12 (397) Chesapeake Invite 22 1252 Cash Crop SE 10 (471) Chesapeake Invite 12 (397) Colorado Cup 4 (384) Old Dominion Q. 23 1087 Dire Wolf MA 2 (455) No Surf 4 (384) Cazenovia 17 (248) Heavyweights 24 1085 Prairie Fire NC 6 (653) Colorado Cup 11 (432) Heavyweights 25 1011 Florida United SE 9 (511) Colorado Cup 1 (500) Old Dominion Q. 26 1010 Boost Mobile SW 8 (555) Club Terminus 2 (455) Cal State 27 1007 Medicine Men MA 12 (397) Heavyweights 5 (354) Old Dominion Q. 9 (256) Cazenovia 28 986 Mephisto NE 7 (602) US Open 4 (384) Cazenovia 29 888 Voodoo NW 10 (471) Colorado Cup 3 (417) San Diego Slammer 30 865 Sprawl SW 9 (511) Heavyweights 5 (354) San Diego Slammer 31 835 Buzz Bullets 3 (835) West Coast Cup 32 833 Garuda NE 8 (555) Heavyweights 8 (278) Cazenovia 33 768 Clapham 4 (768) Chesapeake Invite 34 686 Oaks SW 5 (354) Cal State 14 (332) Heavyweights 35 656 Castle NC 5 (354) Mot. Throwdown 15 (302) Heavyweights 36 653 Euforia 6 (653) US Open 37 632 Sheet Metal 5 (354) No Surf 8 (278) Cazenovia 38 594 Beachfront Property GL 3 (417) Mot. Throwdown 20 (177) Heavyweights 39 575 Space City Ignite SC 7 (301) San Diego Slammer 16 (274) Heavyweights 40 562 Chico 6 (326) Cal State 10 (236) San Diego Slammer 41 555 Plex SC 8 (555) Colorado Cup 42 555 Ragnarok 8 (555) US Open 43 534 Gridlock SW 8 (278) Cal State 9 (256) San Diego Slammer 44 500 Ulysse 1 (500) Cazenovia 45 471 Brickyard GL 10 (471) Heavyweights 46 471 Furious George NW 10 (471) Club Terminus 47 467 Midnight Meat Train GL 7 (301) No Surf 14 (166) Mot. Throwdown 48 458 Lake Effect GL 7 (301) Mot. Throwdown 21 (157) Heavyweights 49 455 Tanasi SE 2 (455) Old Dominion Q. 50 455 Powderhogs NW 2 (455) Col. Cup noTCT 51 453 Madador 10 (236) No Surf 11 (217) Mot. Throwdown 52 435 BD Air Show SW 10 (236) Cal State 12 (199) San Diego Slammer 53 432 Oakland MA 11 (432) Chesapeake Invite 54 417 Boneyard 3 (417) Old Dominion Q. 55 417 Choice City Hops 3 (417) Col. Cup noTCT 56 417 Madcow Y 3 (417) No Surf 57 405 Inception-Red 4 (384) Col. Cup noTCT 30 (21) Heavyweights 58 399 CAKti 11 (217) No Surf 13 (182) Mot. Throwdown 59 384 Madcow X 4 (384) No Surf 60 363 Phoenix NE 13 (363) Colorado Cup 61 354 Sweet Roll SC 5 (354) Col. Cup noTCT 62 354 The Nights Watch NE 5 (354) Cazenovia 63 326 Grand Trunk 6 (326) No Surf 64 326 Vanier Wildcats 6 (326) Cazenovia 65 326 Floodwall 6 (326) Old Dominion Q. 66 326 Enigma GL 6 (326) Mot. Throwdown 67 301 The Ghosts 7 (301) San Diego Slammer 68 301 Swell 7 (301) Old Dominion Q. 69 278 Old Growth 8 (278) Cal State 70 278 Burnside 8 (278) Old Dominion Q. 71 278 Jurassic Shark GL 8 (278) Mot. Throwdown 72 278 Maverick 8 (278) No Surf 73 274 Lancaster MA 16 (274) Colorado Cup 74 256 Journeymen 9 (256) Cal State 75 256 Grantham U. 9 (256) No Surf 76 256 VAlhalla 9 (256) Old Dominion Q. 77 256 Impulse 9 (256) Mot. Throwdown 78 237 Hustle 10 (236) Mot. Throwdown 32 (1) Heavyweights 79 236 Triforce 10 (236) Old Dominion Q. 80 236 Jester 10 (236) Cazenovia 81 231 Spoiler 12 (199) Mot. Throwdown 29 (32) Heavyweights 82 223 Haymaker GL 18 (223) Heavyweights 83 217 Brawl SW 11 (217) San Diego Slammer 84 199 ROY 12 (199) No Surf 85 199 Centretown Gunners 12 (199) Cazenovia 86 199 Warriors of Rad 12 (199) Cazenovia 87 199 Gnarwhal NC 19 (199) Heavyweights 88 194 INfamous 16 (137) Mot. Throwdown 27 (57) Heavyweights 89 182 Stonefish NE 13 (182) Cazenovia 90 166 Youngbloods NE 14 (166) Cazenovia 91 151 Flying Pig 15 (151) Mot. Throwdown 92 137 Freaks Uv Nature SE 22 (137) Heavyweights 93 137 Firebird 16 (137) Cazenovia 94 137 Throw'n Together 16 (137) Cazenovia 95 134 Illusion NC 17 (124) Mot. Throwdown 31 (10) Heavyweights 96 119 Mufasa 23 (119) Heavyweights 97 112 MicroMachines 18 (112) Mot. Throwdown 98 102 Mad Men 24 (102) Heavyweights 99 100 Rust Belt War Bonds 19 (100) Mot. Throwdown 100 89 Salvage 3 20 (89) Mot. Throwdown 101 86 H1N1 NC 25 (86) Heavyweights 102 71 yogosbo 26 (71) Heavyweights 103 44 City Park Ultimate NC 28 (44) Heavyweights
Suppose such a ranking was used for bid allocation in USA. The next table compares the number of bid that were allocated per region for the USAU Championshipwith with the number of teams per region in the top 16 of the above ranking.
| Region | Total bid allocated | Teams in top 16 |
|---|---|---|
| GL | 2 | 2 |
| MA | 1 | 1 |
| NC | 1 | 2 (+1) |
| NE | 3 | 3 |
| NW | 2 | 2 |
| SC | 2 | 3 (+1) |
| SE | 3 | 2 (-1) |
| SW | 2 | 1 (-1) |
Of course, the relative number of points for tournaments is important. It must be well studied and tested to reach the good equilibrium. For example, maybe 400 or 600 points is best suited for second level tournaments instead of 500.
Dessins et calculs d'orbites avec Sage d'une fonction associée à l'algo LLL
04 février 2014 | Catégories: sage | View CommentsAujourd'hui avait lieu une rencontre de l'ANR DynA3S. Suite à une présentation de Brigitte Vallée, j'ai codé quelques lignes en Sage pour étudier une fonction qu'elle a introduite. Cette fonction est reliée à la compréhension de la densité des termes sous-diagonaux dans l'exécution de l'algorithme LLL.
D'abord voici mon fichier: brigitte.sage.
Pour utiliser ce fichier, il faut d'abord l'importer dans Sage en utilisant la commande suivante. En ligne de commande, ça fonctionne bien. Dans le Sage notebook, je ne sais plus trop si la commande load permet encore de le faire (?):
sage: %runfile brigitte.sage # not tested
On doit générer plusieurs orbites pour visualiser quelque chose, car les orbites de la fonction sont de taille 1, 2 ou 3 en général avant que la condition d'arrêt soit atteinte. Ici, on génère 10000 orbites (les points initiaux sont choisis aléatoirement et uniformément dans \([0,1]\times[-0.5, 0.5]\). On dessine les derniers points des orbites:
sage: D = plusieurs_orbit(10000)
Note: la plus longue orbite est de taille 3
sage: A = points(D[0], color='red', legend_label='derniers')
sage: B = points(D[1], color='blue', legend_label='avant derniers')
sage: C = points(D[2], color='black', legend_label='2e avant derniers')
sage: G = A + B + C
sage: G.axes_labels(("$x$", r"$\nu$"))
sage: title = r"$(x,\nu) \mapsto (\frac{x}{(x+\nu^2)^2},\frac{\nu}{(x+\nu^2)})$"
sage: G.show(title=title, xmax=2)

Un raccourci pour faire à peu près le même dessin que ci-haut:
sage: draw_plusieurs_orbites(10000).show(xmax=2)
On dessine des histogrammes surperposés de la densité de ces points une fois projetés sur l'axe des \(\nu\):
sage: histogrammes_nu(10000, nbox=10)

Le dessin semble indiquer que la densité non uniforme semble provenir simplement par les points \((x,\nu)\) tels que \(x\leq 1\).
On dessine des histogrammes superposés de la densité de ces points une fois projetés sur l'axe des \(x\) (on donne des couleurs selon la valeur de \(\nu\)):
sage: histogrammes_x(30000, nbox=5, ymax=1500, xmax=8)

Le dessin semble indiquer que la densité ne dépend pas de \(\nu\) pour \(x\geq 1\).
My opinion on the USAU Ranking Algorithm
25 janvier 2014 | Catégories: ultimate | View CommentsUSA Ultimate recently annonced modifications made to their ranking algorithm for 2014 Season:
Boulder, Colo. (January 17, 2014) – USA Ultimate, the national governing body for the sport of ultimate in the United States, and the organization’s Algorithm Working Group announced today improvements to the algorithm used to calculate rankings in the college and club divisions. The new model, USA Ultimate Top 25 (version 2.0) was devised by the volunteer Algorithm Working Group with guidance from members of the USA Ultimate competition department.
The USA Ultimate Rankings (version 2.0) is fully described here and reactions already started on the ultiworld blog. To me, the modifications are technical improvement and fix some issues of the algorithm. But, in my opinion, the inherent problem of the algorithm remains. Below are my thoughs that I shared on the ultiworld blog.
To me the principal weekness of the actual USAU Ranking algorithm is that it doesn't see the structure of tournaments. For the algorithm used by USAU, a tournament is just a bunch of random games. The algorithm does not see the difference between the saturday morning game and the sunday afternoon final (apart the one day difference which won't affect much). Suppose the two finalist teams of a tournament appear to be in the same pool on the Saturday. The algorithm will consider both games to decide the best. Any human will say the best team is the one who wons the final!
This is why I believe that any Ranking Algorithms in Ultimate should not use the results of games but the results of tournaments. Ultimate frisbee is such a sport that games are played during tournaments and this fact must be considered. The output of a tournament is an ordering of teams (may not be a total order if not all placements games are played) and this is what the algorithm should take as an input.
Moreover, ranking is not only about ranking. It can be a great source of motivation for team to improve (this is why USAU, if they want team to improve, should look into this) but it will do so only if at least two conditions are satisfied : (1) the ranking must be predictable and (2) the ranking must reward what is the most difficult to acheive : winning the final of a tournament. And these are exactly the weaknesses of the actual ranking algorithm whose recursive computation part makes it completely unpredictable and which is blind on the importance of games.
If the ranking system is predictable, then you know in advance that winning a certain game will give you exactly 200 pts for example and this is the amount you need to become #1 in the country, then it will be one more motivation to win the game.
Other sports use such system : tennis ATP ranking, Formula 1, etc. Moreover, it exists in Ultimate as well : Quebec Ultimate Federation is using such a system since more than 5 years to rank Ultimate teams. Team get points according to their final placement. Winners of "Grand Slam" tournament get 1000 pts. Other smaller tournaments gives less points. The final ranking considers the sum of the best three results during the season. For more info, the system is described in this text.
« Previous Page -- Next Page »
