The Oldenburger infinite sequence [O39] \[ K = 1221121221221121122121121221121121221221\ldots \] also known under the name of Kolakoski, is equal to its exponent trajectory. The exponent trajectory \(\Delta\) can be obtained by counting the lengths of blocks of consecutive and equal letters: \[ K = 1^12^21^22^11^12^21^12^21^22^11^22^21^12^11^22^11^12^21^22^11^22^11^12^21^12^21^22^11^12^21^12^11^22^11^22^21^12^21^2\ldots \] The sequence of exponents above gives the exponent trajectory of the Oldenburger sequence: \[ \Delta = 12211212212211211221211212\ldots \] which is equal to the original sequence \(K\). You can define this sequence in Sage:

sage: K = words.KolakoskiWord()
sage: K
word: 1221121221221121122121121221121121221221...
sage: K.delta()          # delta returns the exponent trajectory
word: 1221121221221121122121121221121121221221...

There are a lot of open problem related to basic properties of that sequence. For example, we do not know if that sequence is recurrent, that is, all finite subword or factor (finite block of consecutive letters) always reappear. Also, it is still open to prove whether the density of 1 in that sequence is equal to \(1/2\).

In this blog post, I do some computations on its abelian complexity \(p_{ab}(n)\) defined as the number of distinct abelian vectors of subwords of length \(n\) in the sequence. The abelian vector \(\vec{w}\) of a word \(w\) counts the number of occurences of each letter: \[ w = 12211212212 \quad \mapsto \quad 1^5 2^7 \text{, abelianized} \quad \mapsto \quad \vec{w} = (5, 7) \text{, the abelian vector of } w \]

Here are the abelian vectors of subwords of length 10 and 20 in the prefix of length 100 of the Oldenburger sequence. The functions abelian_vectors and abelian_complexity are not in Sage as of now. Code is available at trac #17058 to be merged in Sage soon:

sage: prefix = words.KolakoskiWord()[:100]
sage: prefix.abelian_vectors(10)
{(4, 6), (5, 5), (6, 4)}
sage: prefix.abelian_vectors(20)
{(8, 12), (9, 11), (10, 10), (11, 9), (12, 8)}

Therefore, the prefix of length 100 has 3 vectors of subwords of length 10 and 5 vectors of subwords of length 20:

sage: p100.abelian_complexity(10)
3
sage: p100.abelian_complexity(20)
5

I import the OldenburgerSequence from my optional spkg because it is faster than the implementation in Sage:

sage: from slabbe import KolakoskiWord as OldenburgerSequence
sage: Olden = OldenburgerSequence()

I count the number of abelian vectors of subwords of length 100 in the prefix of length \(2^{20}\) of the Oldenburger sequence:

sage: prefix = Olden[:2^20]
sage: %time prefix.abelian_vectors(100)
CPU times: user 3.48 s, sys: 66.9 ms, total: 3.54 s
Wall time: 3.56 s
{(47, 53), (48, 52), (49, 51), (50, 50), (51, 49), (52, 48), (53, 47)}

Number of abelian vectors of subwords of length less than 100 in the prefix of length \(2^{20}\) of the Oldenburger sequence:

sage: %time L100 = map(prefix.abelian_complexity, range(100))
CPU times: user 3min 20s, sys: 1.08 s, total: 3min 21s
Wall time: 3min 23s
sage: from collections import Counter
sage: Counter(L100)
Counter({5: 26, 6: 26, 4: 17, 7: 15, 3: 8, 8: 4, 2: 3, 1: 1})

Let's draw that:

sage: labels = ('Length of factors', 'Number of abelian vectors')
sage: title = 'Abelian Complexity of the prefix of length $2^{20}$ of Oldenburger sequence'
sage: list_plot(L100, color='green', plotjoined=True, axes_labels=labels, title=title)

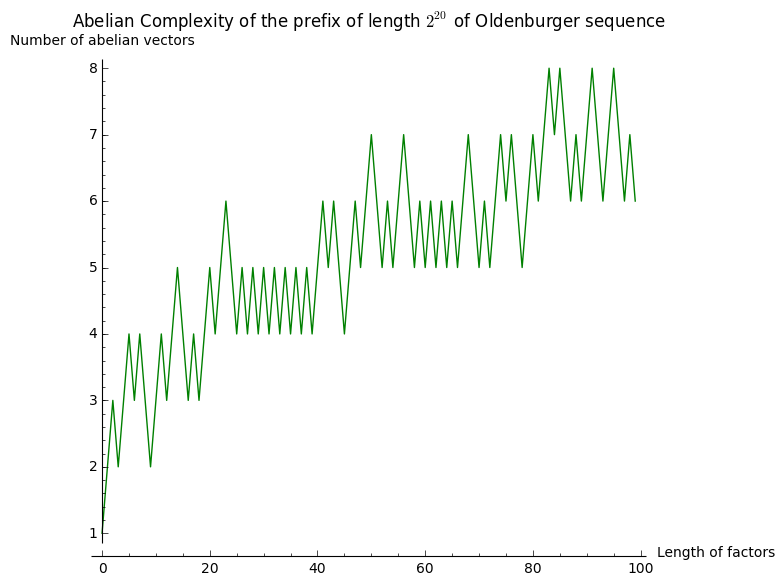
It seems to grow something like \(\log(n)\). Let's now consider subwords of length \(2^n\) for \(0\leq n\leq 12\) in the same prefix of length \(2^{20}\):

sage: %time L20 = [(2^n, prefix.abelian_complexity(2^n)) for n in range(20)]
CPU times: user 41 s, sys: 239 ms, total: 41.2 s
Wall time: 41.5 s
sage: L20
[(1, 2), (2, 3), (4, 3), (8, 3), (16, 3), (32, 5), (64, 5), (128, 9),
(256, 9), (512, 13), (1024, 17), (2048, 22), (4096, 27), (8192, 40),
(16384, 46), (32768, 67), (65536, 81), (131072, 85), (262144, 90), (524288, 104)]

I now look at subwords of length \(2^n\) for \(0\leq n\leq 23\) in the longer prefix of length \(2^{24}\):

sage: prefix = Olden[:2^24]
sage: %time L24 = [(2^n, prefix.abelian_complexity(2^n)) for n in range(24)]
CPU times: user 20min 47s, sys: 13.5 s, total: 21min
Wall time: 20min 13s
sage: L24
[(1, 2), (2, 3), (4, 3), (8, 3), (16, 3), (32, 5), (64, 5), (128, 9), (256,
9), (512, 13), (1024, 17), (2048, 23), (4096, 33), (8192, 46), (16384, 58),
(32768, 74), (65536, 98), (131072, 134), (262144, 165), (524288, 229),
(1048576, 302), (2097152, 371), (4194304, 304), (8388608, 329)]

The next graph gather all of the above computations:

sage: G = Graphics()
sage: legend = 'in the prefix of length 2^{}'
sage: G += list_plot(L24, plotjoined=True, thickness=4, color='blue', legend_label=legend.format(24))
sage: G += list_plot(L20, plotjoined=True, thickness=4, color='red', legend_label=legend.format(20))
sage: G += list_plot(L100, plotjoined=True, thickness=4, color='green', legend_label=legend.format(20))
sage: labels = ('Length of factors', 'Number of abelian vectors')
sage: title = 'Abelian complexity of Oldenburger sequence'
sage: G.show(scale=('semilogx', 2), axes_labels=labels, title=title)

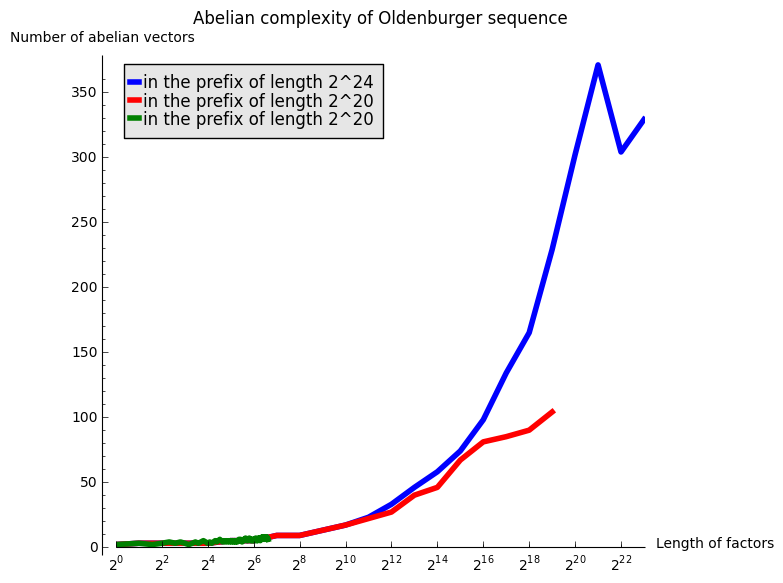
A linear growth in the above graphics with logarithmic \(x\) abcisse would mean a growth in \(\log(n)\). After those experimentations, my hypothesis is that the abelian complexity of the Oldenburger sequence grows like \(\log(n)^2\).

Voici quelques dessins de l'évolution du Circuit québécois d'ultimate 4 contre 4 (CQU4).

Croissance de la participation aux tournois

Le premier ci-bas montre le nombre de participations à chaque tournoi de la saison. C'est un dessin que j'avais déjà fait et que j'ai simplement mis à jour. Pendant la saison 2013-2014, il y a eu un total de 427 participations aux tournois du CQU4. La croissance est de 30 à 60 participations de plus par années. On peut donc imaginer qu'il y aura plus de 500 participations dans le circuit d'ici deux à trois ans si la tendance se maintient.

Croissance en hauteur vs largeur

Il y deux façons d'accueillir de nouvelles équipes:

1. créer de nouveaux tournois (croissance en largeur),
2. augmenter la taille des tournois existants (croissance en hauteur).

On a été plutôt négligeant sur la croissance en largeur avec la création d'un seul nouveau tournoi au cours des cinq dernières années (de 7 tournois en 2008-2009, il y en avait que 8 en 2013-2014). Par contre, augmenter la taille des tournois existants, ça on sait faire. Inspiré par le Mars Attaque qui grandit en repoussant toutes les limites, nous avons assis la croissance des cinq dernières années en acceptant toujours plus d'équipes dans les tournois. Alors qu'il y avait en moyenne 30 équipes par tournois en 2008-2009, il y en avait 50 la saison dernière. Le dessin suivant illustre la croissance des deux façons:

Les données ayant permis de faire les graphes ci-haut sont dans le tableau ci-bas:

Le problème est qu'une moyenne de 50 équipes par tournoi semble être une limite physique associé à la capacité d'accueil d'un plateau de soccer intérieur (divisé en 9 terrains). Ça ne semble pas être un problème à Québec où l'AJJUQ parvient à louer un deuxième puis un troisième plateau et atteindre les 27 terrains. Mais peut-on faire la même chose dans toutes les villes du Québec? Par exemple à Sherbrooke où je ne sais pas s'il existe un deuxième plateau de soccer intérieur?

Il faut l'admettre, la croissance en hauteur atteindra sa limite. Soit on l'a déjà atteinte, soit on l'atteindra cette année, soit ce sera l'année prochaine. Mais, dans tous les cas, on l'atteindra. La seule solution à ce moment-là sera de croître en largeur en créant de nouveaux tournois. Et plus on attend, plus le déficit à rattraper sera grand. À mon avis, il faudrait qu'il y ait un nouveau tournoi par année pour accueillir la croissance moyenne annuelle de 30 à 60 participations à un tournoi vue dans le premier graphique ci-haut. Or, on a cinq années de non croissance à rattraper... Je suggère de commencer dès maintenant!

Croissance de l'adhésion au CQU4

Le graphique suivant illustre le nombre d'équipes participant à 1, 2 ou à 3 tournois ou plus. Dans le CQU4, un grand nombre d'équipe participent à un seul tournoi. C'est très encourageant, car cela signifie qu'il y a une place dans le CQU4 pour l'initiation à la compétition et pour la participation à un tournoi local. Depuis toujours, une quinzaine d'équipes participent à deux tournois. Ce sont des équipes entre deux qui participeront peut-être à trois tournois l'année suivante qui sait? Il faudrait faire plus d'investigation à leur sujet...

Puis, un nombre de plus en plus grand en font trois ou plus. Une équipe qui fait 3 tournois ou plus est une équipe qui a adhéré au CQU4 et qui désire probablement se hisser parmi les 32 meilleures équipes au Québec. Pendant trois ans de 2011 à 2013, une cinquantaine d'équipe participaient à au moins 3 tournois. Puis, l'année dernière, il y a eu une forte progression avec près de 70 équipes participant à 3 tournois ou plus. Notez aussi qu'en moyenne les équipes participant à plus de 3 tournois participent à 4 tournois (voir plus bas pour les chiffres).

On peut donc se demander à quoi pensent ces 70 équipes en ce moment. Ce sont des équipes qui voudront encore cette année participer au CQU4 dans le but de se qualifier pour le CCQU4. Le problème est que les tournois du Grand Chelem sont saturés et qu'il n'y aura pas assez de place pour eux.

Les chiffres ayant permis de construire le graphique précédent sont ci-bas. On compte le nombre d'équipes selon le nombre de tournois participés. En 2006-07, 35 équipes avaient participé à 1 tournoi, 7 équipes avaient participé à 2 tournois, 9 équipes avaient participé à 3 tournois, etc.

Ce que je pense des récentes modifications annoncées par la FQU

Plusieurs modifications ont été annoncées récemment par la FQU pour la saison 2014-2015. Voici quelques commentaires en vrac:

• Je déplore qu'il n'y ait pas de nouveaux tournois encore une fois cette année. À quand un tournoi à Lanaudière (FUL)? Drumondville? Granby? Alma? Victoriaville? À quand un tournoi de Série C (200 points) à Montréal? Québec? Trois-Rivières? Sherbrooke?
• Le pointage des tournois de Série B n'a pas été modifié. Il devrait y avoir des échelles pour 200, 400, 600, 800 et 1000 points données à l'équipe gagnante. De plus, les tournois de Série B devraient donner plus de points pour alléger la pression sur les tournois du Grand Chelem.
• Je n'aime pas tellement la décision de sortir le Mars Attaque du CQU4. À l'heure où on se demande comment accueillir les 100 prochaines participations qui viendront pour les trois prochaines années, on enlève un tournoi qui donnait des points à 120 équipes dans le CQU4. Je pense qu'on cherche vraiment à déplaire à toutes les équipes qui ne parviendront pas à atteindre les objectifs qu'ils s'étaient fixés.
• Je crois que le fait de sortir le Mars Attaque du CQU4 freinera sa croissance. Cette année, les équipes iront par habitude. Mais, selon moi, dans les prochaines années, ils auront du mal à avoir autant d'équipes que les années passées. Toute la pression sera mise sur le nouveau "dernier" tournoi du CQU4: le Coup de Foudre. Les équipes qui auront fait un seul tournoi voudront absolument se qualifier pour le Coup de Foudre. Aussi, les équipes qui voudront corriger un précdent mauvais résultat parmi le Movember et le Bye Bye vondront aussi participer au Coup de Foudre. Finalement toutes les équipes vondront participer au Coup de Foudre, car ce sera la dernière chance pour améliorer son classement et possiblement se qualifier pour le CCQU4. On peut imaginer que 70 à 90 équipes voudront participer au Coup de Foudre. Mais combien y aura-t-il de places?
• En fait, je pense que le CQU4 a toujours été plus valorisé que le CCQU4 lui-même. Plusieurs ont souvent trouvé que le CCQU4 était trop tard en avril, etc. Pour cette raison la FQU a décidé de le déplacer au Mars Attaque et donc de compter seulement 2 tournois plutôt que 3 dans la saison. Je pense qu'il existe d'autres solutions à ce problème telle que faire le CCQU4 dehors au mois d'avril ou simplemenent annuler le CCQU4. L'équipe championne est celle qui termine première au classement. Et on utilise le classement du CQU4 pour qualifier les équipes pour le Championnat canadien. Ce n'est pas nécessaire que les équipes passent par le CCQU4 pour aller aux championnats canadiens. On pourrait décider que le top 5 du CQU4 vont aux championnats canadiens et que le 6-32 vont aux championnats québécois organisé en mème temps que les championnats canadiens.
• Je pense qu'un classement du CQU4 en comptant les trois meilleurs résultats est plus authentique que si on compte que les deux meilleurs résultats. Il y a peut-être des surprises à prévoir de ce côté. On verra. J'ai pensé au système d'échelle de pointage en fonction de trois tournois. J'ai fait plusieurs simulations et tout qui me garrantissent que ça marche bien pour trois tournois. Mais, si ça avait été deux tournois seulement, je l'aurais probablement fait l'échelle différement. En comptant deux tournois, il faut que l'échelle dégringole moins vite pour permettre aux équipes de dépasser les autres (il leur reste juste une chance pour les dépasser). En comparaison, au tennis (ATP et WTA ranking) l'échelle dégringole très très très vite. C'est OK, car on compte les 18 meilleurs résultats et il te reste donc une chance de dépasser Serena Williams si elle gagne le premier tournoi. Mais si on en compte que deux, il ne faudrait pas que Serena soit assurée d'être classée dans le top 8 juste parce qu'elle a fait une finale tsé...

These is a summary of the functionalities present in slabbe-0.1 optional Sage package. It depends on version 6.3 of Sage because it uses RecursivelyEnumeratedSet code that was merged in 6.3. It contains modules on digital geometry, combinatorics on words and more.

Install the optional spkg (depends on sage-6.3):

sage -i http://www.liafa.univ-paris-diderot.fr/~labbe/Sage/slabbe-0.1.spkg

In each of the example below, you first have to import the module once and for all:

sage: from slabbe import *

To construct the image below, make sure to use tikz package so that view is able to compile tikz code when called:

sage: latex.add_to_preamble("\\usepackage{tikz}")
sage: latex.extra_preamble()
'\\usepackage{tikz}'

Draw the part of a discrete plane

sage: p = DiscretePlane([1,pi,7], 1+pi+7, mu=0)
sage: d = DiscreteTube([-5,5],[-5,5])
sage: I = p & d
sage: I
Intersection of the following objects:
Set of points x in ZZ^3 satisfying: 0 <= (1, pi, 7) . x + 0 < pi + 8
DiscreteTube: Preimage of [-5, 5] x [-5, 5] by a 2 by 3 matrix
sage: clip = d.clip()
sage: tikz = I.tikz(clip=clip)
sage: view(tikz, tightpage=True)

Draw the part of a discrete line

sage: L = DiscreteLine([-2,3], 5)
sage: b = DiscreteBox([0,10], [0,10])
sage: I = L & b
sage: I
Intersection of the following objects:
Set of points x in ZZ^2 satisfying: 0 <= (-2, 3) . x + 0 < 5
[0, 10] x [0, 10]
sage: I.plot()

Double square tiles

This module was developped for the article on the combinatorial properties of double square tiles written with Ariane Garon and Alexandre Blondin Massé [BGL2012]. The original version of the code was written with Alexandre.

sage: D = DoubleSquare((34,21,34,21))
sage: D
Double Square Tile
  w0 = 3032321232303010303230301012101030   w4 = 1210103010121232121012123230323212
  w1 = 323030103032321232303                w5 = 101212321210103010121
  w2 = 2321210121232303232123230301030323   w6 = 0103032303010121010301012123212101
  w3 = 212323032321210121232                w7 = 030101210103032303010
(|w0|, |w1|, |w2|, |w3|) = (34, 21, 34, 21)
(d0, d1, d2, d3)         = (42, 68, 42, 68)
(n0, n1, n2, n3)         = (0, 0, 0, 0)
sage: D.plot()

sage: D.extend(0).extend(1).plot()

We have shown that using two invertible operations (called SWAP and TRIM), every double square tiles can be reduced to the unit square:

sage: D.plot_reduction()

The reduction operations are:

sage: D.reduction()
['SWAP_1', 'TRIM_1', 'TRIM_3', 'SWAP_1', 'TRIM_1', 'TRIM_3', 'TRIM_0', 'TRIM_2']

The result of the reduction is the unit square:

sage: unit_square = D.apply(D.reduction())
sage: unit_square
Double Square Tile
  w0 =     w4 =
  w1 = 3   w5 = 1
  w2 =     w6 =
  w3 = 2   w7 = 0
(|w0|, |w1|, |w2|, |w3|) = (0, 1, 0, 1)
(d0, d1, d2, d3)         = (2, 0, 2, 0)
(n0, n1, n2, n3)         = (0, NaN, 0, NaN)
sage: unit_square.plot()

Since SWAP and TRIM are invertible operations, we can recover every double square from the unit square:

sage: E = unit_square.extend(2).extend(0).extend(3).extend(1).swap(1).extend(3).extend(1).swap(1)
sage: D == E
True

Christoffel graphs

This module was developped for the article on a d-dimensional extension of Christoffel Words written with Christophe Reutenauer [LR2014].

sage: G = ChristoffelGraph((6,10,15))
sage: G
Christoffel set of edges for normal vector v=(6, 10, 15)
sage: tikz = G.tikz_kernel()
sage: view(tikz, tightpage=True)

sage: L = [(1,3), (2,3), (3,1), (3,2), (3,3)]
sage: E = ExtensionType1to1(L, alphabet=(1,2,3))
sage: E
  E(w)   1   2   3
   1             X
   2             X
   3     X   X   X
 m(w)=0, ordinary
sage: E.is_ordinaire()
True

sage: p23 = WordMorphism({1:[1,2,3],2:[2,3],3:[3]})
sage: e = ExtensionType1to1([(1,2),(2,3),(3,1),(3,2),(3,3)], [1,2,3])
sage: e
  E(w)   1   2   3
   1         X
   2             X
   3     X   X   X
 m(w)=0, not ord.
sage: A,B = e.apply(p23)
sage: A
  E(3w)   1   2   3
    1
    2         X   X
    3     X   X   X
 m(w)=1, not ord.
sage: B
  E(23w)   1   2   3
    1          X
    2
    3              X
 m(w)=-1, not ord.

sage: K = KolakoskiWord()
sage: K
word: 1221121221221121122121121221121121221221...
sage: %time K[10^5]
CPU times: user 1.56 ms, sys: 7 µs, total: 1.57 ms
Wall time: 1.57 ms
1
sage: %time K[10^6]
CPU times: user 15.8 ms, sys: 30 µs, total: 15.8 ms
Wall time: 15.9 ms
2
sage: %time K[10^8]
CPU times: user 1.58 s, sys: 2.28 ms, total: 1.58 s
Wall time: 1.59 s
1
sage: %time K[10^9]
CPU times: user 15.8 s, sys: 12.4 ms, total: 15.9 s
Wall time: 15.9 s
1

sage: K = words.KolakoskiWord()
sage: %time K[10^5]
CPU times: user 779 ms, sys: 25.9 ms, total: 805 ms
Wall time: 802 ms
1

Since two years I wrote thousands of line of private code for my own research. Each module having between 500 and 2000 lines of code. The code which is the more clean corresponds to code written in conjunction with research articles. People who know me know that I systematically put docstrings and doctests in my code to facilitate reuse of the code by myself, but also in the idea of sharing it and eventually making it public.

I did not made that code into Sage because it was not mature enough. Also, when I tried to make a complete module go into Sage (see #13069 and #13346), then the monstrous never evolving #12224 became a dependency of the first and the second was unofficially reviewed asking me to split it into smaller chunks to make the review process easier. I never did it because I spent already too much time on it (making a module 100% doctested takes time). Also, the module was corresponding to a published article and I wanted to leave it just like that.

Getting new modules into Sage is hard

In general, the introduction of a complete new module into Sage is hard especially for beginners. Here are two examples I feel responsible for: #10519 is 4 years old and counting, the author has a new work and responsabilities; in #12996, the author was decouraged by the amount of work given by the reviewers. There is a lot of things a beginner has to consider to obtain a positive review. And even for a more advanced developper, other difficulties arise. Indeed, a module introduces a lot of new functions and it may also introduce a lot of new bugs... and Sage developpers are sometimes reluctant to give it a positive review. And if it finally gets a positive review, it is not available easily to normal users of Sage until the next release of Sage.

Releasing my own Sage package

Still I felt the need around me to make my code public. But how? There are people (a few of course but I know there are) who are interested in reproducing computations and images done in my articles. This is why I came to the idea of releasing my own Sage package containing my public research code. This way both developpers and colleagues that are user of Sage but not developpers will be able to install and use my code. This will make people more aware if there is something useful in a module for them. And if one day, somebody tells me: "this should be in Sage", then I will be able to say : "I agree! Do you want to review it?".

Old style Sage package vs New sytle git Sage package

Then I had to chose between the old and the new style for Sage packages. I did not like the new style, because

• I wanted the history of my package to be independant of the history of Sage,
• I wanted it to be as easy to install as sage -i slabbe,
• I wanted it to work on any recent enough version of Sage,
• I wanted to be able to release a new version, give it to a colleague who could install it right away without changing its own Sage (i.e., updating the checksums).

Therefore, I choose the old style. I based my work on other optional Sage packages, namely the SageManifolds spkg and the ore_algebra spkg.

Content of the initial version

The initial version of the slabbe Sage package has modules concerning four topics: Digital geometry, Combinatorics on words, Combinatorics and Python class inheritance.

For installation or for release notes of the initial version of the spkg, consult the slabbe spkg section of the Sage page of this website.

1. Quelles villes ou villages du Québec, ou d’ailleurs dans le monde, pourraient servir d’inspiration pour Lac-Mégantic ? Pourquoi ?

Montpellier (France).

Un quartier piéton de un kilomètre carré dans le centre de la ville. C'est lorsque j'ai habité dans cette ville en 2009-2010 que j'ai réalisé à quel point les voitures sont bruyantes et désagréables. Au Québec, comme les voitures sont partout, on les tolère et on ne réalise pas qu'elles nous stressent. Un endroit où les voitures ne circulent pas permet aux citoyens de se réapproprier l'espace public (air, sol, son). Les terrasses des resto prennent la rue. On s'entend parler. On peut discuter. Et moins d'exhaust de char dans notre assiette.

Autour du quartier piéton, il y a des embouteillages de voitures causés par les accès rendus difficiles. Je suis retourné en 2013 et vous ne devinerez pas ce que la ville de Montpellier a fait comme changement dans l'une de ces rues embouteillées : le nombre de voies pour les voitures est passé de 2 à 1 au profit d'une piste cyclable. Les embouteillages sont rendus si pire que la vitesse moyenne des voitures est de 16 km/h. Il vaut mieux se rendre au centre-ville à pied, prendre le tram ou prendre le vélo. Voilà une ville qui a compris comment régler les embouteillages de voitures : les rendre pire! Comme ça les gens trouvent de meilleures solutions de transport souvent plus vertes et plus écolos.

Pour s'inspirer justement et pour en savoir plus sur une ville qui se voit en 2040 en train de relever les défis de demain et non en 1960 en train de subir les erreurs du passé, je vous invite à consulter les pages web de la ville de Montpellier à propos de l'urbanisme, du déplacement actif, de la circulation et d'aménagement du territoire.

2. Quels types de projets ou d'activités pourraient améliorer la qualité de vie à Lac-Mégantic ?

Il faut surtout éviter que l'urbanisme fasse de Lac-Mégantic une ville pour le char. Si l'accès aux services principaux de Lac-Mégantic est facilité pour les voitures et compliqué ou dangereux pour les piétons, je comprends que le monde choisissent d'habiter à Frontenac ou dans une autre banlieue parce qu'il n'y a pas d'avantage à habiter proche et de toute façon, il faut s'y rendre en char.

Or, je sais que Lac-Mégantic est capable de concevoir son urbanisme en pensant très bien aux voitures et très peu aux piétons. D'où l'importance d'en parler. En effet, avant les événements du 6 juillet, il y a eu la construction d'un nouveau centre sportif. Y aller en voiture, c'était génial : tu t'y rends, tu te stationnes, tu rentres. Par contre à vélo ou à pied, c'était compliqué et dangereux. D'abord, mélanger vélo et piéton sur la même voie, ça coûte peut-être moins cher, mais c'est dangereux : les deux n'ont vraiment pas la même vitesse. Ensuite, l'accès pour les piétons et les vélos nécessitait de traverser la rue à la toute fin pour se rendre au bâtiment. À mon avis, c'était dangereux (un piéton qui regarde le bâtiment traverse en diagonal et ne voit pas la voiture qui lui rentre dedans), inefficace (une traversée piéton dans le goulot d'entrée pour les voitures).

Il faut que les concepteurs se mettent à la place des piétons dans les plans qu'ils conçoivent. C'est important, c'est pour les résidents de notre ville!

3. Quelle thématique principale, quelle ambiance, devrait ressortir du futur centre-ville?

Un centre-ville où on passe d'une activité à l'autre en marchant. Pour ce faire, il faut des rues piétonnes, des trottoirs des deux côtés pour les rues qui ne peuvent pas être que piétonnes, des axes cyclables utiles. Par utile, je veux dire qui partent des quartiers résidentiels et qui se rendent devant la porte des magasins. Les stationnements à vélos doivent être nombreux et mieux placés que les stationnement pour voitures. Par mieux placés, je veux dire plus proche des entrées des magasins. Bien sûr, ça prend aussi des arbres.

Par définition, les axes cyclables utiles seront utilisés par les résidents. C'est bien une piste cyclable qui fait le tour du lac et qui se rendent dans le parc des vétérans ou pourquoi pas jusqu'au bout de la rue d'Orsennens. Les cul-de-sac, c'est bien pour les touristes et les citoyens le dimanche après-midi. Mais, une piste cyclable on le sait, c'est pas juste pour les touristes, ça peut aussi être aussi un moyen de transport pour aller d'un point A (maison) à un point B (service, épicerie, centre-ville).

Je pense qu'à Lac-Mégantic, il manque des pistes cyclables qui se rendent dans les quartiers résidentiels. Il faudrait une piste cyclable qui fasse toute la rue Papineau pour aller chercher les résidents de ce quartier. C'est pas si cher dans une telle rue : il suffit de réasphalter un peu et mettre de la peinture (voir la piste cyclable de la rue Boyer ou Rachel à Montréal). Il faudra aussi une piste cyclable qui relie le cégep avec le centre-ville. Il faut réfléchir un peu pour choisir les bonnes rues. Peut-être que la rue dollard serait la bonne, je ne sais pas.

Ensuite, ça prend des pistes cyclables qui se rendent aux services, aux restaurants (le centre-ville par exemple) mais aussi qui se rendent dans les lieux de travail importants tel que le parc industriel. Est-ce que les pistes cyclables qui longent la rivière déboucheront sur le parc industriel? Il faut! Il faut que les employés des usines puissent se rendre à vélo à leur travail en évitant si possible la rue villeneuve.

4. Vous avez d’autres idées ou commentaires ? N’hésitez pas, cet espace vous appartient.

Un cercle de pierre à Lac-Mégantic! Quand je suis allé en Irlande il y a qq années, j'ai visité des alignements de roche vieux de 6000 ans (à la StoneEdge) et des cercles de pierres. Les cercles de pierre sont toujours placé à un endroit où on voit bien l'horizon. Les alignement dans le cercle sont faits en fonction du lieu à l'horizon où se couche le soleil. Les alignements de l'entrée du cercle avec les autres pierres indiquent le solstice d'été (le coucher de soleil le plus à droite sur l'horizon), le solstice d'hiver (le coucher de soleil le plus à gauche à l'horizon) et les équinoxes de printemps et d'automne (au milieu). Ils étaient utilisés peut-être comme calendrier pour prédire les saisons, le temps de la récolte, etc.

Quand, je suis revenu, je m'étais dit que ce serait bon d'en faire un à Lac-Mégantic. J'avais pensé à deux lieux : près de la piste cyclable en bas de la polyvalente. C'est un endroit où on voit bien l'horizon. Aussi, j'avais pensé à la pelouse entre le centre sportif et le centre-ville. De cet endroit, on voyait aussi bien l'horizon. C'est une idée qui ne coût pas grand chose (il y avait déjà un empilement de roches près du centre sportif) et qui peut devenir un lieu de recueillement, d'apprentissage (un écriteau explique les alignements choisi pour le cercle de pierre de Lac-Mégantic, explique les premiers alignements de pierre faits il y a 6000 ans, etc.) et de réflexion (on regarde le coucher du soleil).