Animation des solutions d'un puzzle de Florent Hivert

22 juillet 2011 | Catégories: animation, sage | View Comments

On veut placer les pièces suivantes dans un carré 8 par 8.

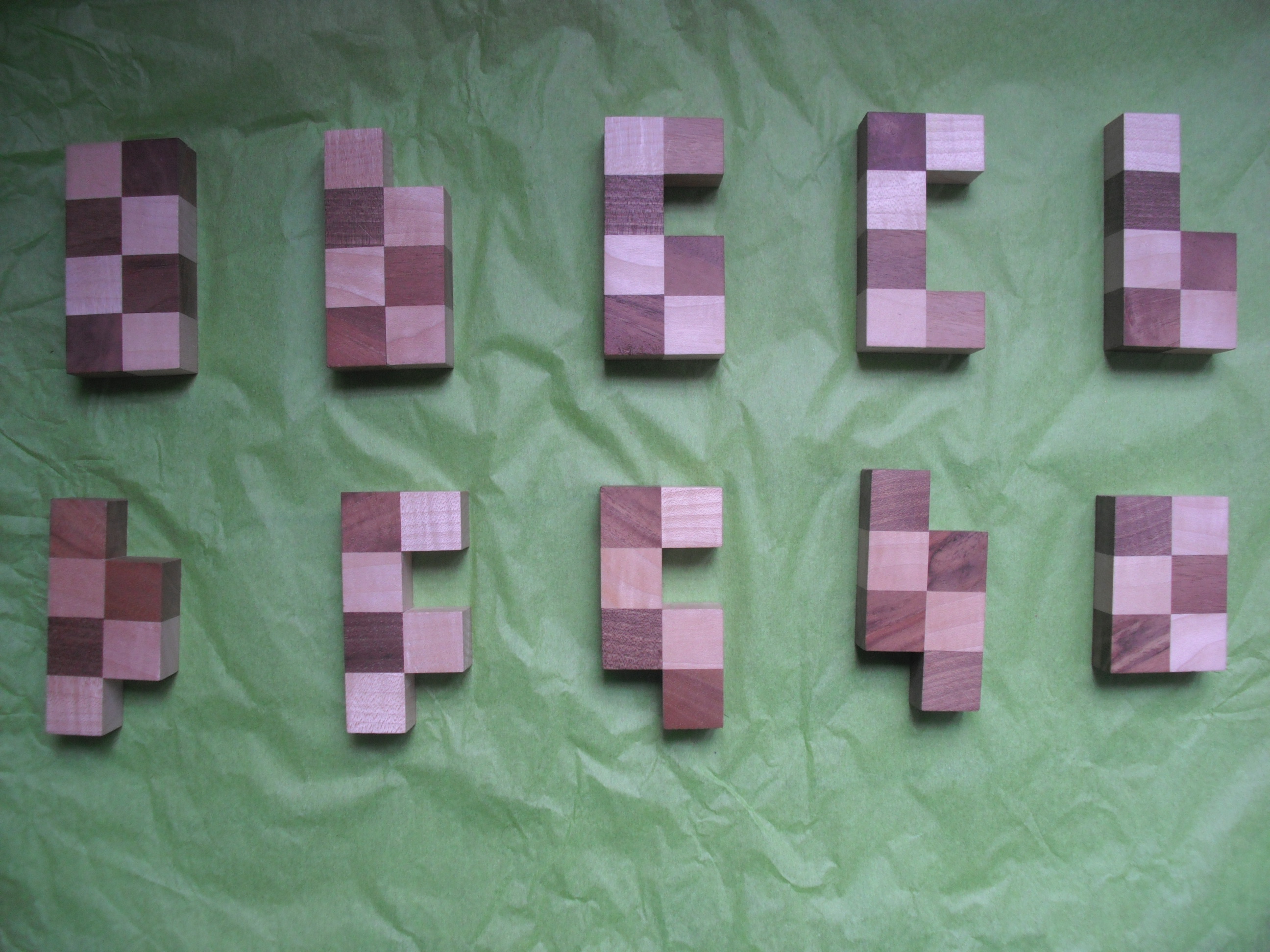
En utilisant sage-4.7 muni des patchs du ticket #11379 et avec les commandes suivantes, on peut trouver une solution et même les calculer toutes:

sage: from sage.combinat.tiling import Polyomino, TilingSolver
sage: L = []
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3)], 'yellow'))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2)], "black"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,3)], "gray"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,3)],"cyan"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1)],"red"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,1),(1,2)],"blue"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,1),(1,3)],"green"))
sage: L.append(Polyomino([(0,1),(0,2),(0,3),(1,0),(1,1),(1,3)],"magenta"))
sage: L.append(Polyomino([(0,1),(0,2),(0,3),(1,0),(1,1),(1,2)],"orange"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(1,0),(1,1),(1,2)],"pink"))
sage: T = TilingSolver(L, (8,8), reflection=True)
sage: T.number_of_solutions()
328

Ainsi (sans tenir compte de la non adjacence des carrés blancs et noirs), il y a 328 solutions. Les voici en animation:

sage: a = T.animate()
sage: a
Animation with 328 frames
sage: a.show(delay=50, iterations=1)

Chaque solution est répétée 8 fois (les 4 rotations et les 4 rotations de l'image miroir), ainsi il n'y a que 41 solutions vraiment distinctes:

sage:: factor(328)
8 * 41

J'ai aussi codé:

sage: a = T.animate('incremental', stop=300)

où une seule pièce est enlevée ou ajoutée à la fois ce qui permet vraiment de visualiser les liens dansants de Knuth (rafraîchir le navigateur pour faire recommencer l'animation):

Sébastien Labbé

Animation des solutions d'un puzzle de Florent Hivert