Blogue

Faire une animation en 3D avec Sage

18 janvier 2012 | Catégories: animation, sage | View Comments

En Sage, il est relativement facile de créer des animations d'images en 2D. Pour cela, il suffit d'utiliser la commande animate qui s'occupera d'utiliser les commandes plus compliquées ffpmeg ou convert. Plusieurs exemples sont disponibles dans la documentation de Sage ou sur le wiki de Sage.

Par contre, il n'est pas encore possible de faire une animation d'objets graphiques 3D. Le logiciel Jmol, utilisé dans Sage pour faire de la visualisation 3D le permet, car les chimistes l'utilise pour faire des animations 3D de molécules complexes, mais cette fonctionalité n'a pas encore été exportée dans Sage. En juin dernier, j'en ai parlé à Jonathan Gutow, responsable des mises à jour de Jmol dans Sage, mais il doit d'abord régler d'autres problèmes plus importants.

En attendant, il est possible de s'en sortir en utilisant Tachyon plutôt que Jmol. Je rappelle que Tachyon est utilisé dans Sage pour créer des images png d'objets graphiques 3d. Ensuite, on peut immiter ce que la fonction animate fait pour créer une animation d'une scène 3d.

Pour illustrer la méthode par un exemple, faisons une animation de la technique des liens dansants de Knuth pour trouver les solutions du puzzle Quantumino.

Dans un répertoire, créer un fichier Sage video_quantumino.sage qui contiendra le code suivant:

from sage.games.quantumino import QuantuminoSolver
import itertools

def animate(block=4, stop=400, angle=pi/200.0, nb_pareil=5):
    r"""
    This functions creates plenty of png images in the images folder.

    INPUT:

    - ``block`` - integer between 0 and 16, the block to put aside

    - ``stop`` - integer, number of iterations

    - ``angle`` - number, rotation angle (radian) between each frame

    - ``nb_parei`` - integer, number of frame per iteration

    OUTPUT:

    Plenty of png images in the images folder.
    """
    q = QuantuminoSolver(block)
    it = q.solve(partial='incremental')
    i = 0
    for solution in itertools.islice(it, stop):
        G = solution.show3d()
        G += sphere((4,7,1),size=0.1,opacity=0) # hack to stabilize the frame
        G += sphere((0,7,0),size=0.1,opacity=0) # hack to stabilize the frame
        #G += sphere((2,4,1),size=10,opacity=0) # pas opaque pantoute

        for _ in range(nb_pareil):
            H = G.rotateZ(angle * i)

            filename = 'images/image%s.png' % i
            H.save(filename, frame=False, aspect_ratio=1)
            print "Création du fichier %s" % filename

            i += 1

animate(4, stop=20, angle=pi/200.0, nb_pareil=5)

Créer les images à l'aide de Sage >= 4.7.2

mkdir images
sage video_quantumino.sage

Aller dans le répertoire images et faites ensuite:

cd images
ffmpeg -y -f image2 -r 20 -i image%d.png video.mpg

Le résultat est ici (bloc numéro 4 mis de côté, 200 itérations, angle=\(\pi\)/200, 5 images par itérations, total de 1000 images):

Read and Post Comments

Animation des solutions d'un puzzle de Florent Hivert

22 juillet 2011 | Catégories: animation, sage | View Comments

On veut placer les pièces suivantes dans un carré 8 par 8.

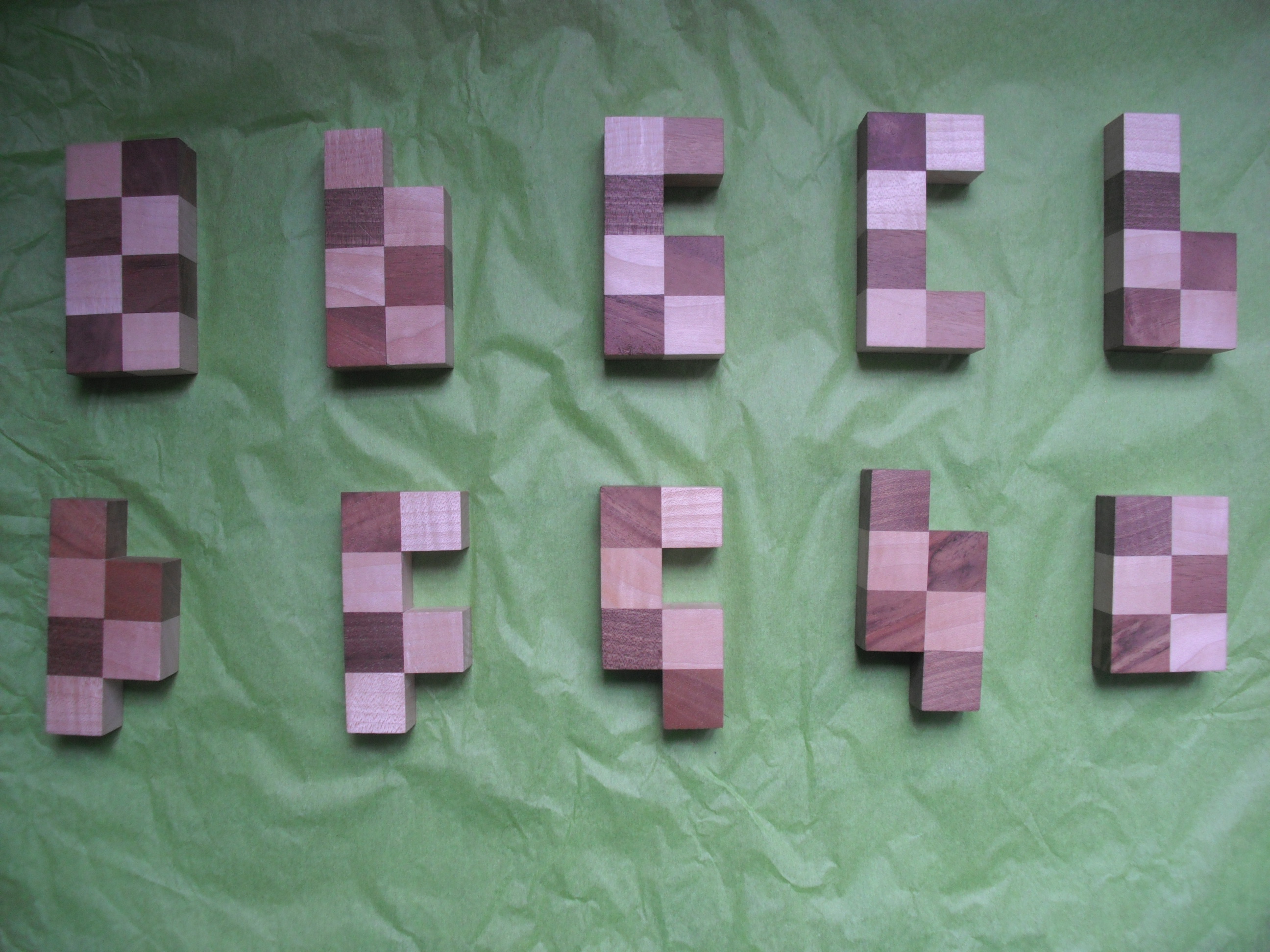
En utilisant sage-4.7 muni des patchs du ticket #11379 et avec les commandes suivantes, on peut trouver une solution et même les calculer toutes:

sage: from sage.combinat.tiling import Polyomino, TilingSolver
sage: L = []
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3)], 'yellow'))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2)], "black"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,3)], "gray"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,3)],"cyan"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1)],"red"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,1),(1,2)],"blue"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,1),(1,3)],"green"))
sage: L.append(Polyomino([(0,1),(0,2),(0,3),(1,0),(1,1),(1,3)],"magenta"))
sage: L.append(Polyomino([(0,1),(0,2),(0,3),(1,0),(1,1),(1,2)],"orange"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(1,0),(1,1),(1,2)],"pink"))
sage: T = TilingSolver(L, (8,8), reflection=True)
sage: T.number_of_solutions()
328

Ainsi (sans tenir compte de la non adjacence des carrés blancs et noirs), il y a 328 solutions. Les voici en animation:

sage: a = T.animate()
sage: a
Animation with 328 frames
sage: a.show(delay=50, iterations=1)

Chaque solution est répétée 8 fois (les 4 rotations et les 4 rotations de l'image miroir), ainsi il n'y a que 41 solutions vraiment distinctes:

sage:: factor(328)
8 * 41

J'ai aussi codé:

sage: a = T.animate('incremental', stop=300)

où une seule pièce est enlevée ou ajoutée à la fois ce qui permet vraiment de visualiser les liens dansants de Knuth (rafraîchir le navigateur pour faire recommencer l'animation):

Read and Post Comments

The Tamer and the Lion (done with Xavier Provençal)

20 novembre 2009 | Catégories: animation, sage | View Comments

A tamer wants to escape within a circle without being eaten by a lion who lives on the circle. The speed of the lion is 4 times that of the tamer. How can the tamer escape? There is a nice and clever solution in 2d, but does the naive solution where the tamer always moves oppositely to the lion works? In November 2009, a small script written in Sage by Xavier Provençal and Sébastien Labbé in Montpellier answers the question. To create the animation, download the script tamer.sage and run the commands:

sage: load tamer.sage
sage: l = range(0,1200,10)
sage: a = anime(l)
sage: a
Animation with 120 frames
sage: show(a)

How can the tamer escape? Can you find the solution?

Read and Post Comments

Fibonacci Tiles

01 juillet 2009 | Catégories: animation, sage | View Comments

The first 7 Fibonacci Tiles:

sage: path_op = dict(rgbcolor='red', thickness=1)
sage: fill_op = dict(rgbcolor='blue', alpha=0.3)
sage: options = dict(pathoptions=path_op, filloptions=fill_op, endarrow=False, startpoint=False)
sage: G = [words.fibonacci_tile(i).plot(**options) for i in range(7)]
sage: a = animate(G)
sage: a.show(delay=150)

Read and Post Comments