Quelques opinions sur l'organisation de l'ultimate en France
02 juillet 2013 | Catégories: ultimate | View CommentsJ'observe l'organisation de l'ultimate en France depuis quelques temps. Au moins depuis 2006, année où j'ai rencontré un certain Français joueur d'ultimate à Sherbrooke. En septembre 2007, il m'avait fait visiter les bureaux de la fédération française à Versailles. La visite avait été très inspirante, car à l'époque, au Québec, nous commencions la vie de la Fédération québécoise. Le site web de la Fédération québécoise a été créé le mois suivant en octobre 2007. Puis, nous nous étions inspiré du classement des équipes françaises d'ultimate sur plage (mais aussi de l'ATP et de la Formule 1!) dans la création du Circuit québécois d'ultimate 4 contre 4 (CQU4).
Des séjours plus longs par la suite, une année à Montpellier et une autre à Paris depuis l'automne dernier, m'ont permis de rencontrer les membres de la communauté d'ultimate française. Nous avons toujours été très bien accueillis et avons développé de nombreuses amitiés qui perdurent! Ces séjours m'ont aussi fait vivre de l'intérieur l'organisation de l'ultimate en France.
Le but de ce texte est de rassembler et expliquer les opinions que j'ai développées au cours des dernières années sur l'organisation de l'ultimate en France. Plus spécifiquement, je m'intéresse à la structure des compétitions et au modèle global de développement des joueurs. L'objectif premier est de pouvoir par la suite en discuter dans la communauté. Mes opinions pourront mener à une amélioration de l'organisation de l'ultimate en France seulement si la communauté partage le même opinion. Étant donné que j'ai le défaut de focusser sur les aspects à améliorer (à mes yeux bien sûr) et de négliger tout ce qui va bien, voici les thèmes que je vais aborder dans les différentes sections de ce texte.
- Absence de structure d'accueil des nouveaux joueurs (absence de ligues récréatives!)
- Choix de l'équipe championne nationale
- Niveau de jeu féminin
- Championnat de France par phases
- Pour un championnat de France avec phase décisive
- Sélection de l'équipe de France pour les WUCC et les WUGC
- Mur 1: Les divisions
- Importance de l'exactitude du classement
- Mur 2: La licence
Absence de structure d'accueil des nouveaux joueurs (absence de ligues récréatives!)
Le niveau de jeu d'une communauté forme une pyramide où chaque niveau repose sur un niveau plus bas. De plus, la pyramide sera aussi haute qu'elle sera large à sa base. Dix joueurs et joueuses élites sont basés sur une centaine de joueurs et joueuses de compétitions qui sont basés sur un millier de joueurs et joueuses récréatifs. Où sont les joueurs récréatifs en France? Il n'y en a pas. Ou plutôt, j'en ai vus, mais il n'y a pas de structure d'accueil pour eux. Les joueurs récréatifs en France sont les joueurs débutants qui viennent aux pratiques d'une équipe de compétition et qui ont l'impression de déranger, car ils ne sont pas encore assez bons ou parce qu'ils ne sont pas encore assez mordus pour aller faire 3 heures de route pour participer au prochain tournoi du club.
Alors que l'objectif d'une association au Québec est principalement d'organiser des ligues pour les joueurs récréatifs, l'objectif d'un club en France est de participer et performer lors des championnats de France. Les rencontres hebdomadaires des clubs sont des pratiques et non des matchs. Difficile de devenir mordu de l'ultimate quand les rencontres locales sont des exos plutôt que du jeu et que les erreurs sont moins tolérées.
Le cheminement de tous les joueurs de compétition au Québec est d'abord d'avoir joué des matchs d'ultimate hebdomadaires dans la ligue d'une association (ou une ligue scolaire pour les plus jeunes) pendant un an ou deux. Ensuite, parmi tous ces joueurs, plusieurs deviennent mordus et un certain pourcentage d'entre eux (peut-être 10%) le deviennent assez pour faire des pratiques les soirs de semaine avec une équipe de compétition et faire de la route pour participer à des tournois compétitifs pendant les fins de semaine.
Je peux donc difficilement imaginer que le niveau de jeu en France augmente tellement sans que la fédération sinon les clubs organisent des ligues locales tenues une fois par semaine afin d'offrir une structure d'accueil en tout temps de l'année pour les débutants et joueurs récréatifs de leur région où le plaisir de jouer prime d'abord et avant tout.
Choix de l'équipe championne nationale
Un des rôles d'une fédération est de nommer une équipe championne à chaque année éventuellement dans plus d'une division. Ces équipes nommées par la fédération sont susceptibles de représenter le pays dans les compétitions internationales. Au Québec, aux États-Unis et au Canada, le champion national est décidé lors d'un match ultime entre deux équipes qui sont parvenues à se rendre à ce match final. Le match final est bien sûr un match d'ultimate fait en suivant les règles de jeu de la fédération, car c'est bien l'équipe championne d'ultimate que l'on veut choisir. La date du match ultime est bien connue de tous: un dimanche autour du 15 avril pour le CCQU4, autour du 15 juillet pour le CQU7, autour du 15 août pour les CUC et autour du 30 octobre pour les USAU. Toutes les équipes savent que c'est à cette date qu'on doit être la meilleure au pays. Dans tous les cas, les règles pour atteindre ce match sont connues de tous et le processus pour l'atteindre dure au plus 3 mois. Ce qui veut dire qu'une équipe peut se former trois mois à l'avance à partir de rien et devenir champion national (au Canada la date limite pour s'inscrire et soumettre un alignement est le 15 juin, au États-Unis la date limite est à la fin août; donc deux mois à l'avance dans les deux cas). Je ne dis pas que la tâche est facile, mais elle est mathématiquement et administrativement possible. Cela fait en sorte qu'une équipe peut se rendre aussi loin que son talent le permet.
Niveau de jeu féminin
Je suis moins au fait de la division féminine, donc, je peux moins en parler. Mais, je ne veux pas taire ici qu'il y a énormément de travail à faire dans cette division. Dans les clubs que j'ai vus dans le sud de la France, le nombre de filles n'est pas assez grand pour que les clubs puissent participer dans la catégorie féminine. Du coup, les filles jouent.... avec les gars dans la catégorie masculine. Ce n'est pas si mal, car la plupart du temps chaque club joue avec deux ou trois filles et celles-ci jouent une contre l'autre. Mais, il y a toujours un club constitué exclusivement d'hommes qui va se faire un plaisir d'avoir comme stratégie de lancer une longue passe sur le gars qui est surveillé par une fille. Je pense qu'une réflexion s'impose ici et qu'il serait plus logique de jouer dans la catégorie mixte avec un certain nombre obligatoire de filles sur le terrain plutôt que de jouer en catégorie masculine. Mais bon, vous allez me dire qu'en France le mixte, c'est à l'automne, le masculin et le féminin, c'est au printemps. Et moi, je demanderai pourquoi est-ce qu'on impose cela aux équipes et plus généralement comment proposez-vous alors d'augmenter le niveau de jeu féminin en France?
Championnat de France par phases
Dans la division masculine, le Championnat de France est divisé en trois phases. Contrairement aux États-Unis, au Canada ou au Québec, il n'y a pas de match décisif pour décider qui entre deux équipes sera championne de France. Plutôt, le championnat se fait en trois phases, c'est-à-dire trois tournois, et une moyenne pondérée des résultats permet de choisir l'équipe championne de France. On comprend donc que la dernière et troisième phase du Championnat de France ne pourra jamais être aussi excitante que les Championnats canadiens, que les Championnats américains ou que les Championnats du monde, car les deux premières phases ensemble ont un poids deux fois plus fort que la dernière dans la pondération. Aussi, la finale tant attendue entre deux équipes peut simplement ne pas avoir lieu. Je ne sais pas ce qui s'est passé dans les années précédentes ni ce qui se passera dans les prochaines si la Fédération française ne change pas le système, mais cette année, je sais ce qui s'est passé pour l'avoir vécu. En 2013, les trois phases ont été remportées par trois équipes différentes (Friselis en mars, Tchac en avril et Izno en mai). Comment est-ce que la fédération française choisit alors l'équipe championne je vous le demande?
- un tirage au hasard entre les trois équipes
- un ou des matchs de ping pong
- un ou des matchs d'ultimate
- une pondération quelconque des résultats finaux
Un match de ping pong (B), ce serait absurde, car on veut choisir la meilleure équipe d'ultimate. Un match d'ultimate (C) pour choisir la meilleure équipe d'ultimate, non plus, ce serait trop logique peut-être. Entre un tirage au sort (A) et une pondération des résultats (D), la fédération française choisit (D) une pondération des résultats. Erreur selon moi! Pourquoi c'est une erreur à mon avis? En organisant un championnat sur trois phases, la fédération envoie un message ambigu et reçoit une réponse ambigüe. En effet, les équipes ont répondu chacune à leur manière en atteignant des sommets (peak) dans leur développement à des moments différents. Friselis a atteint son sommet en début de saison, suivi de Thac en avril. Finalement, UV et Izno ont atteint leur sommet à la fin de la saison en atteignant la finale de la dernière phase après avoir éliminé les champions et vice-champions de France en demi-finale. Si la fédération française choisissait un moment unique dans la saison pour choisir les champions nationaux (comme c'est le cas au Canada, au Québec et aux États-Unis), alors les équipes connaîtraient leur sommet tous en même temps. Ce serait alors à mon avis le meilleur moment pour décider qui est la meilleure équipe de France en choisissant l'équipe victorieuse d'un match ultime.
Pour un championnat de France avec phase décisive
Une solution pas trop compliquée (qui ne chamboulerait pas tout le système) serait de conserver les deux premières phases pour en faire une saison régulière, soit sous le même format, soit encore sous le format d'un tournoi à la ronde réparti sur deux fins de semaine. Le classement final de la saison régulière permettrait de se qualifier dans une plus ou moins bonne position pour la phase finale: la phase 3. Par exemple, la phase 3 pourrait être organisée de la façon suivante : PoolA = 1-3-5-7; Pool B = 2-4-6-8; Pool C = 9-10-11-12. Le samedi, un tournoi à la ronde est organisé pour chaque pool. Ça nous donne trois matchs par équipes. Le samedi en fin de journée, les deux derniers des pools A et B jouent contre les équipes du pool C en pré-quart-de-finales. Les gagnants des pré-quarts jouent contre A1, A2, B1, B2 en quart-de-finales le dimanche matin. Les perdants des pré-quarts jouent pour les places 9 à 12 le dimanche. Après les quarts, ce sont les demi-finales, et ensuite une finale ultime où deux équipes jouent un match pour être champion de France.
Cette solution aurait l'avantage de mettre de la pression sur les meilleures équipes (donc de les forcer à devenir meilleures). En effet, dans un tel système, les équipes classées en positions 3, 4, 5, 6 n'auront pas besoin de s'éliminer entres elles en quart-de-finales comme c'est le cas actuellement avant de pouvoir affronter les équipes 1 et 2. Présentement, le système protège les meilleures équipes de France, et tant que ce sera le cas, ces meilleures équipes n'auront pas besoin de s'améliorer et seront toujours désavantagées au niveau international.
Sélection de l'équipe de France pour les WUCC et les WUGC
Les championnats internationaux comme les WUCC et les WUGC sont une excellente opportunité pour augmenter le niveau de jeu dans son pays. Pourquoi? Comment? Est-ce que la seule participation à un tournoi international d'une durée d'une semaine permet d'augmenter son niveau de jeu? Bien sûr que non! Tout est dans le processus et dans la préparation à la participation aux tournois internationaux. Au Canada, les équipes qui participeront aux WUCC en Italie à l'été 2014 seront choisies selon les résultats des Championnats canadiens en août 2013. Cela signifie que présentement, plus d'une centaine de joueurs au Québec ont commencé le processus de préparation à l'Italie, parce qu'il ont besoin de se qualifier cette année. Ensuite, les équipes qualifiées en août 2013 auront près d'une année pour se préparer à l'Italie. Ils pourront même refaire des essais libres (ajouter et retirer des joueurs) ce qui poussera chaque joueur à bien s'entraîner et à se dépasser pour rester dans l'équipe. C'est donc dans ce processus qui est commencé à l'hiver 2013 et qui se terminera en Italie à l'été 2014 que plus d'une centaine de joueurs québécois augmenteront leur niveau de jeu ce qui aura pour effet d'augmenter le niveau de jeu de tous les joueurs avec qui et contre qui ils jouent au Québec. Aux vues de tous les bénéfices d'une telle préparation aux Championnats du monde, je ne comprend pas pourquoi la fédération française ne désire pas profiter de ce processus en choisissant si tard (en mai 2014) les équipes françaises qui participeront au WUCC en Italie à l'été 2014.
Un autre argument concerne la difficulté de connaître deux sommets (peaks) dans la même saison. Les spécialistes de l'entraînement peuvent l'expliquer mieux que moi, mais il est difficile pour un athlète et pour une équipe de préparer une saison constituée de deux sommets. On verra donc une équipe française se qualifier pour les WUCC mais être incapable de performer à son meilleur lors des WUCC. Ou encore, il est possible qu'une équipe se préparant "trop" pour les WUCC perde au passage le Championnat de France.
Ceci dit, il semble parfois qu'en France le WUCC et le WUGC ne sont pas tellement plus prestigieux que les équivalents européens EUCC et EUGC. De plus, ces quatre tournois s'alternent aux quatre ans de sorte qu'il y en a un à chaque année. De plus, environ une ou deux équipes françaises par division peut participer à ces tournois. Ce sont donc souvent les mêmes joueurs qui participent à chacun de ces tournois. Ainsi, il semble plus difficile d'avoir des objectifs à long terme vu la multiplicité de ceux-ci. Par exemple, présentement, les meilleures équipes françaises focussent sur la qualification aux Championnats européens par clubs qui aura lieu en septembre 2013. Les Championnats du monde par club d'Italie 2014 sont encore très loin...
Mur 1: Les divisions
Un important problème pour le développement de l'ultimate en France est la présence de divisions. Pour plusieurs raisons.
- Une équipe doit passer au travers d'un processus minimum de trois ans avant de pouvoir devenir championne de France et surtout avant de pouvoir mettre de la pression sur les meilleures équipes.
- Donc, des équipes sont les meilleures non pas pour leur talent et leurs victoires, mais parce qu'elles sont protégées par la séparation en divisions.
- Les meilleures équipes reçoivent ainsi moins de pression par la masse ce qui entraîne qu'elles ne sont pas aussi bonnes qu'elles ne pourraient l'être.
- Les équipes faibles de la division 1 ne sont pas défiées par les équipes fortes de la division 2.
- Les équipes faibles de la division 2 ne sont pas défiées par les équipes fortes des divisions régionales.
- Le flot d'équilibrage entre les divisions à chaque année n'est pas décidé par la force des équipes en présence, mais par une décision a priori d'échange de deux équipes (si je ne me trompe pas). Si pendant une période de six ans, trois équipes par année auraient dû être échangées de division plutôt que seulement deux, cela fait un déficit de 6 équipes à échanger qui s'accumulent dans la division 2 et qui peut continuer de s'accumuler. Le fait que des équipes de division 2 qui montent en division 1 ne finissent pas dernière en division 1 l'année suivante est un signe du déséquilibre des divisions.
- Ainsi, le modèle actuel permet que les équipes de divisions 2 soient plus fortes que des équipes de division 1.
Importance de l'exactitude du classement
L'exactitude d'un système de classement ou d'une séparation des niveaux en plusieurs divisions est ultra importante. L'exactitude, c'est le reflet de la réalité. Si le classement est exact, alors la meilleure équipe sera classée première au classement, la deuxième équipe sera classée deuxième au classement, etc. Si le classement est inexact, alors la meilleure équipe ne sera pas classée première au classement ou encore la 6e meilleure équipe du pays sera bloquée dans une division inférieure, etc. L'exactitude est ultra importante! Pourquoi? Parce que c'est ce qui donne la valeur au classement et aux divisions. Si le système et son classement a une grande valeur et est respectée dans la communauté, alors les joueurs seront d'autant plus motivés à être reconnus et respectés pour le travail et leur effort via leur résultat dans le classement. À l'inverse, si le classement ne reflète pas la réalité, si les meilleures équipes de division 2 sont meilleures que des équipes de division 1, alors "être en division 1" ou encore "être champion de la division 1" n'as pas une aussi grande valeur. Qui dit moins de valeur, dit moins de motivation dans la communauté à atteindre la division 1 ou à atteindre le titre. Donc, un classement ou des divisions qui ne reflètent pas la réalité signifie une progression plus lente du niveau de jeu.
Mur 2: La licence
Pour moi, la licence est un concept très particulier. C'est un concept qui n'existe pas chez nous. En France, c'est ce qui permet d'avoir une assurance sans quoi il est impossible de participer à un tournoi. J'imagine que c'est plutôt difficile de changer cela. Ce que je trouve particulier est l'obligation qui vient avec elle: c'est-à-dire la fidélité à un club. Chez nous (au Québec, au Canada, aux États-Unis), on a aussi la fidélité, mais elle ne vient pas par obligation mais par goût. Les alignements sont gelés dans les trois mois qui précèdent la compétition nationale. En dehors de ces trois mois, il peut se passer à peu près n'importe quoi. Les clubs peuvent se créer, se défaire, etc. En général, les équipes restent stables, mais s'il y a une équipe à créer ou un changement à faire, les règles ne vont pas l'empêcher. Ce qui est bon pour les joueurs et les équipes sera bon pour la fédération.
Conclusion
Voilà, j'ai fait le tour de ce que j'ai en tête concernant l'organisation de l'ultimate en France en m'intéressant plus spécifiquement à la structure des compétitions et au modèle global de développement des joueurs. Merci d'avoir lu ce texte jusqu'au bout. J'espère que j'aurai l'occasion d'en discuter plus longuement avec vous.
À propos du modèle de développement de l'athlète à l'ultimate
10 avril 2013 | Catégories: ultimate | View CommentsLa Fédération québécoise d'ultimate est en train de concevoir son propre modèle de développement de l'athlète, modèle que chaque fédération doit avoir. Dans ce texte, je transmettrai quelques-unes des réflexions que j'ai sur le sujet. Bien sûr, mes réflexions sont limitées et proviennent en grande partie d'une seule source, car ce n'est pas du tout mon sujet de recherche.
Savoir comment développer les meilleurs athlètes est une très grande question et je suis sûr que les réponses qu'on y apporte évolue au fil des années selon les expériences qui s'acquièrent et surtout suites aux erreurs qui sont faites et ce dans tous les sports. Ainsi, je pense que la fédération doit s'appuyer sur ce qui a de mieux. Or, qui possède cette expertise? Qui sont les experts?
À la conférence annuelle d'Ultimate Canada tenue en novembre 2011 à Québec (dont j'avais fait un résumé), Charles Cardinal était le conférencier invité et il avait fait une très bonne présentation. Pour ma part, c'est à ce moment-là que j'ai été sensibilisé pour la première fois à cette question. M. Cardinal, qui avait été longtemps entraîneur de volleyball, nous disait de profiter du fait que nous sommes un jeune sport pour ne pas refaire les erreurs du passé. Cela signifie que nous avons aujourd'hui la responsabilité de connaître quelles sont les erreurs du passé.
Je me souviens qu'il parlait des entraîneurs qui visaient la victoire pour des équipes d'adolescents. Oui, ils obtenaient la victoire. Ils étaient champions québécois, peut-être même champions canadiens à 15 ans, mais ce sont des joueurs qui à 17-18-19 ans abandonnaient le sport, car on les avaient écoeurés pendant l'adolescence.
Un autre exemple dont il avait parlé était à propos des jeunes qui ont une poussée de croissance tardive. Ces jeunes sont souvent mis de côté dans les sélections des équipes élites adolescentes. Par contre, des recherches montrent que ces jeunes peuvent atteindre des niveaux encore plus élevés dans la vingtaine, d'où l'importance de ne pas les mettre de côté.
Il a cité un nombre encore plus grand d'erreurs commises par le passé à ne pas refaire. J'ai réussi à en trouver une liste (Les problèmes dans le sport) sur le site de Au Canada, le sport c'est pour la vie, organisation qui semble avoir réuni les experts que nous cherchons. Ce site contient une foule d'informations dont les modèles de développement à long terme de l'athlète pour plusieurs sports (Consulter nos ressources > Modèles de DLTA canadiens propres à chaque sport).
Sur le même site, on y décrit les 7 stades du Développement à long terme de l’athlète (DLTA) sur lequel le modèle de développement de l'athlète à l'ultimate doit se baser:
- Stade 1 : Enfant actif (0-6 ans)
- Stade 2 : S’amuser grâce au sport (filles 6-8, garçons 6-9)
- Stade 3 : Apprendre à s’entraîner (filles 8-11, garçons 9-12)
- Stade 4 : S’entraîner à s’entraîner (filles 11-15, garçons 12-16)
- Stade 5 : S’entraîner à la compétition (filles 15-21, garçons 16-23)
- Stade 6 : S’entraîner à gagner (filles 18+, garçons 19+)
- Stade 7 : Vie active (participants de tout âge)
Après la conférence de M. Cardinal, à notre table de 5 ou 6 personnes, on devait discuter du contenu propre à l'ultimate dans chacun des stades. Cette discussion m'a fait comprendre que nous sommes aussi capables, à l'ultimate comme dans les autres sports, de faire des erreurs (selon mon opinion personnel). En effet, une des personnes à notre table expliquait qu'en tant qu'entraîneur, il obligerait ses joueurs à lancer que des revers et des lancers droits et interdirait les lancers marteau et autres lancers particuliers. À mon avis, c'est une erreur. On ne veut pas développer des athlètes à l'image de notre génération. On veut développer des athlètes qui seront les meilleurs pour pratiquer l'ultimate. Or dans les règlements de l'ultimate, il n'est pas fait mention de la manière de lancer le disque. Alors pourquoi ajouter de telles interdictions? Au contraire, j'aimerais que la prochaine génération ne possède pas notre handicap et puisse lancer le disque de toutes les façons!
Je désire réitérer un conseil de M. Cardinal au sujet qu'il faut absolument miser sur l'aspect esprit du jeu et communautaire, deux valeurs essentielles à l'ultimate, dans notre approche de développement de l'athlète.
Finalement, je désire terminer en transmettant les réflexions que j'ai eues depuis la conférence de M. Cardinal, c'est-à-dire depuis un an et demi. Je n'ai pas beaucoup d'expérience sur le développement des jeunes joueurs juniors d'ultimate et à quel moment serait-il propice d'apprendre quoi. Par contre, je suis capable de repérer les bons joueurs et les mauvais joueurs autour de moi une fois grands. Ainsi, c'est sous cet angle maintenant que je réfléchis aux habiletés qui doivent être développées en jeune âge et les habiletés pour lesquelles il n'est pas trop tard de développer dans une équipe senior pendant une ou deux saisons pour atteindre un objectif comme gagner les Championnats canadiens.
Pour l'utilisation des logiciels libres
29 mars 2013 | Catégories: logiciel libre, politique | View CommentsLe gouvernement du Québec me déçoit grandement ces jours-ci lorsque je lis dans les nouvelles que nous continuerons de payer pour des logiciels propriétaires alors qu'il existe, en 2013, des logiciels libres qui sont tout aussi bon sinon mieux.
- Québec : les logiciels libres écartés?, Canoe, 11 février 2013
- Un centre d'expertise en logiciel libre, mais un contrat à Microsoft, Radio-Canada, 18 mars 2013
- Québec adopte deux décrets contre le logiciel libre, Le Devoir, 29 mars 2013
Pourtant, le parti au pouvoir sait bien qu'il commet une erreur. En effet, il l'affirmait lui-même l'an dernier à pareil date:
- Québec doit «réduire sa dépendance à Microsoft», dit le PQ, La Presse, 30 mars 2012
Doit-on rappeler les enjeux?
Pour les logiciels libres dans nos écoles
Pour éviter de payer pour qu'une génération complète de citoyens du Québec ne connaissent et ne savent utiliser que des logiciels propriétaires obligeant ainsi toute la société (dont les entreprises) à payer eux aussi chers de licences pour des logiciels.
Pour les logiciels libres au gouvernement
Le gouvernement du Québec ne doit pas payer des millions de dollars (sinon milliards) pour des logiciels propriétaires alors qu'il existe des logiciels équivalents libres et gratuits.
Maîtres chez nous version 2013: pour une expertise québécoise en logiciels libres
La dépendance face à des entreprises étrangères doit être remplacée par une autonomie québécoise et par le développement d'une expertise québécoise en logiciels libres. Nous ne sommes jamais aussi bien servis que par nous-mêmes!
Parce que nous ne sommes plus en 1993
Nous ne sommes plus en 1993. Nous sommes en 2013. Écrire un logiciel de traitement texte, ce n'est pas compliqué. Ce n'est plus nécessaire de payer pour cela! Le logiciel libre existe et c'est gratuit.
Pour le métier de mécanicien automobile, c'est être pour le logiciel libre
Mon père, mon grand-père et mon arrière-grand-père sont et ont été mécaniciens automobiles depuis 1954. Ils ont toujours aimé observer les mécanismes afin de les comprendre, repérer les problèmes et trouver des solutions. Ainsi, ma famille comprendra bien la comparaison suivante.
Si un logiciel était une voiture, un logiciel propriétaire serait une voiture dont l'ouverture du capot serait interdite par la loi et passible de poursuite, dont la réparation ou la modification serait aussi interdite et où les mécaniciens automobiles et autres réparateurs seraient considérés des pirates bandits.
Un logiciel libre permet d'être ouvert, observé, analysé, compris, modifié, amélioré. Je pense que les usagers de logiciels méritent la liberté et devraient bénéficier des informaticiens comme on bénéficie des mécaniciens pour réparer une voiture.
Parce que la souveraineté, ce n'est pas juste un mot
Un parti politique qui prolonge notre dépendance aux logiciels propriétaires ne peut pas prétendre défendre l'indépendance et rester crédible.
Qu'est-ce que le logiciel libre
Un logiciel libre, en plus d'être gratuit, garanti les 4 libertés suivantes:
- Liberté d'utilisation (gratuité)
- Liberté de regarder le code
- Liberté de modifier le code
- Liberté de redistribuer le logiciel possiblement modifié
Qui veut payer pour avoir moins de libertés?
Utiliser un logiciel propriétaire, c'est donc payer pour avoir moins de libertés. Qui est prêt à faire ça?
Pour en savoir plus
Voici un texte ainsi qu'une entrevue de Richard Stallman permettant d'en savoir plus sur les logiciels libres.
Using sage in the new ipython notebook
10 février 2013 | Catégories: ipython, sage | View Comments(NEW: See also the demo I made at the Sage Paris group meeting in March 2014.)
Ticket #12719 (Upgrade to IPython 0.13) was merged into sage-5.7.beta1. This took a lot of energy (see the number of comments in the ticket and especially the number of patches and dependencies). Big thanks to Volker Braun, Mike Hansen, Jason Grout, Jeroen Demeyer who worked on this since almost one year. Note that in December 2012, the IPython project has received a $1.15M grant from the Alfred P. Sloan foundation, that will support IPython development for the next two years. I really like this IPython sage command line interface so it is really good news!
The IPython notebook
Since version 0.12 (December 21 2011), IPython is released with its own notebook. The differences with the Sage Notebook are explained by Fernando Perez, leader of IPython project, in the blog post The IPython notebook: a historical retrospective he wrote in January 2012. One of the differences is that the IPython Notebook run in its own directory whereas each cell of the Sage Notebook lives in its directory. As William Stein says in the presentation Browser-based notebook interfaces for mathematical software - past, present and future he gave last December at ICERM, there are plenty of projects and directions these days for those interfaces.
In May 2012, I tested the same ticket which was to upgrade to IPython 0.12 at that time. Today, I was curious to test it again.
First, I installed sage-5.7.beta4:
./sage -version Sage Version 5.7.beta4, Release Date: 2013-02-09
Install tornado:
./sage -sh easy_install-2.7 tornado
[update March 6th, 2014] Note that some linux user have to install libssl-dev before tornado:
sudo apt-get install libssl-dev
Install zeromq and pyzmq:
./sage -i zeromq ./sage -i pyzmq
Start the ipython notebook:
./sage -ipython notebook [NotebookApp] Using existing profile dir: u'/Users/slabbe/.sage/ipython-0.12/profile_default' [NotebookApp] Serving notebooks from /Users/slabbe/Applications/sage-5.7.beta4 [NotebookApp] The IPython Notebook is running at: http://127.0.0.1:8888/ [NotebookApp] Use Control-C to stop this server and shut down all kernels.
Create a new notebook. One may use sage commands by adding the line from sage.all import * in the first cell.
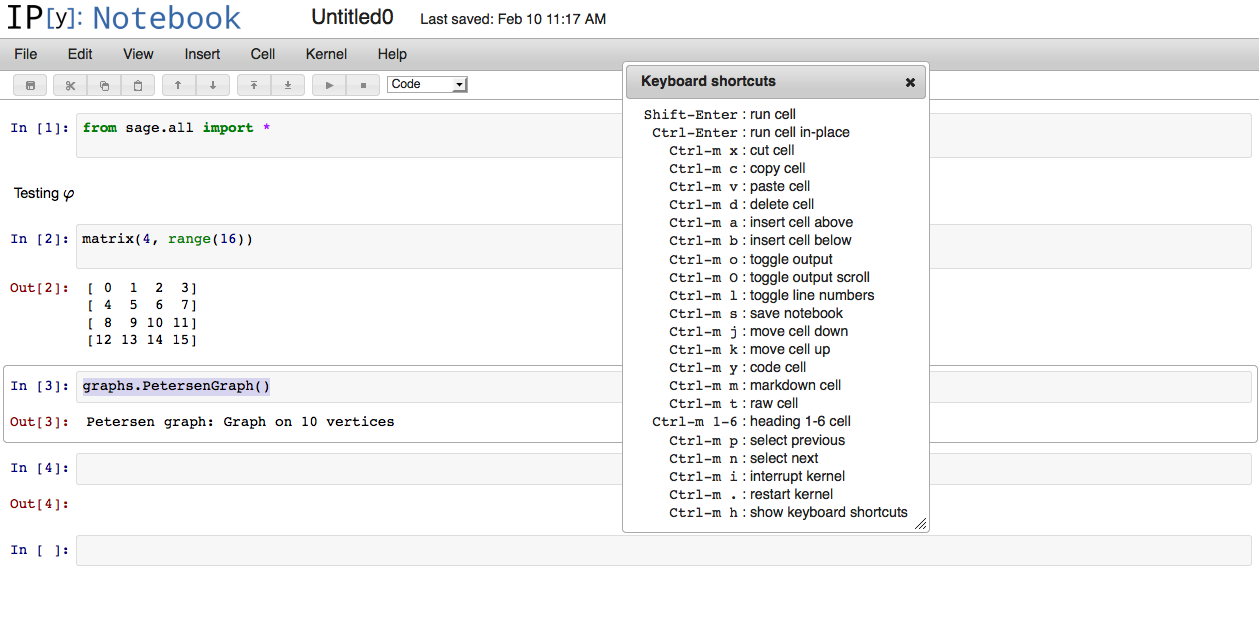
The next things I want to look at are:
- Test the conversion of files from .py to .pynb.
- Test the conversion of files from .rst to .pynb.
- Test the qtconsole.
- Test the parallel computing capacities of the IPython.
Understanding Python class inheritance and Sage coding convention with fruits
28 janvier 2013 | Catégories: python, sage | View CommentsSince Sage Days 20 at Marseille held in January 2010, I have been doing the same example over and over again each time I showed someone else how object oriented coding works in Python: using fruits, strawberry, oranges and bananas.
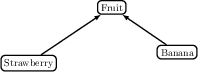
Here is my file: fruit.py. I use to build it from scratch by adding one line at a time using attach command to see what has changed starting with Banana class, then Strawberry class then Fruit class which gathers all common methods.
This time, I wrote the complete documentation (all tests pass, coverage is 100%) and followed Sage coding convention as far as I know them. Thus, I hope this file can be useful as an example to explain those coding convention to newcomers.
One may check that all tests pass using:
$ sage -t fruit.py sage -t "fruit.py" [3.7 s] ---------------------------------------------------------------------- All tests passed! Total time for all tests: 3.8 seconds
One may check that documentation and doctest coverage is 100%:
$ sage -coverage fruit.py ---------------------------------------------------------------------- fruit.py SCORE fruit.py: 100% (10 of 10) ----------------------------------------------------------------------
« Previous Page -- Next Page »
