During Sage Days 31, I worked on the ticket #11459 to implement rst to sws conversion. This post intends to give some documentation about this new feature. Here is an example of a ReStructuredText file calculus.rst:

********
Calculus
********

Let's do some calculus using Sage.

Differentiation
===============

The derivative of $\\sin(x)$ is::

    sage: diff(sin(x), x)
    cos(x)

The derivative of $\\log(x) + x^2$ is::

    sage: diff(log(x) + x^2, x)
    2*x + 1/x

Integration
===========

Sage can integrate $\\int x^3 dx$::

    sage: f = x^3 
    sage: f.integral(x)
    1/4*x^4

Let's compute $\\int x \\sin(x^2) dx$::

    sage: f = x*sin(x^2)
    sage: integral(f,x)
    -1/2*cos(x^2)

Both the files calculus.rst and calculus.html, which was generated from the file calculus.rst using Docutils and the command rst2html.py calculus.rst calculus.html, can be uploaded into the Sage Notebook (copy their URL):

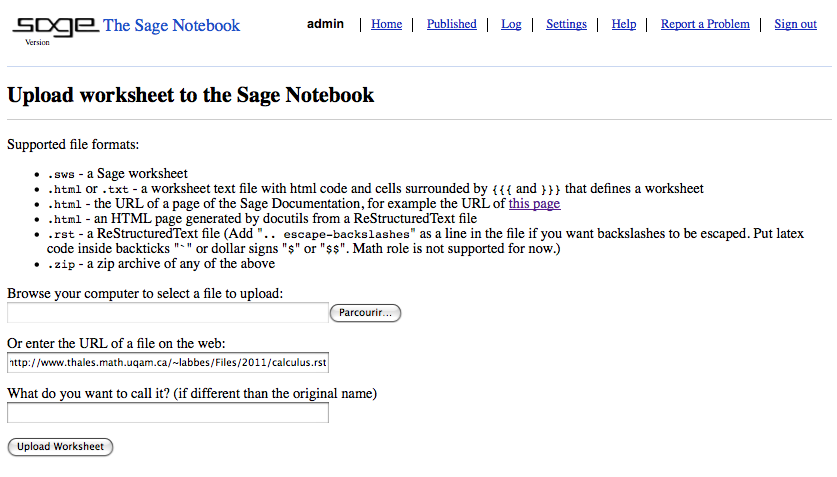
This will create a new worksheet:

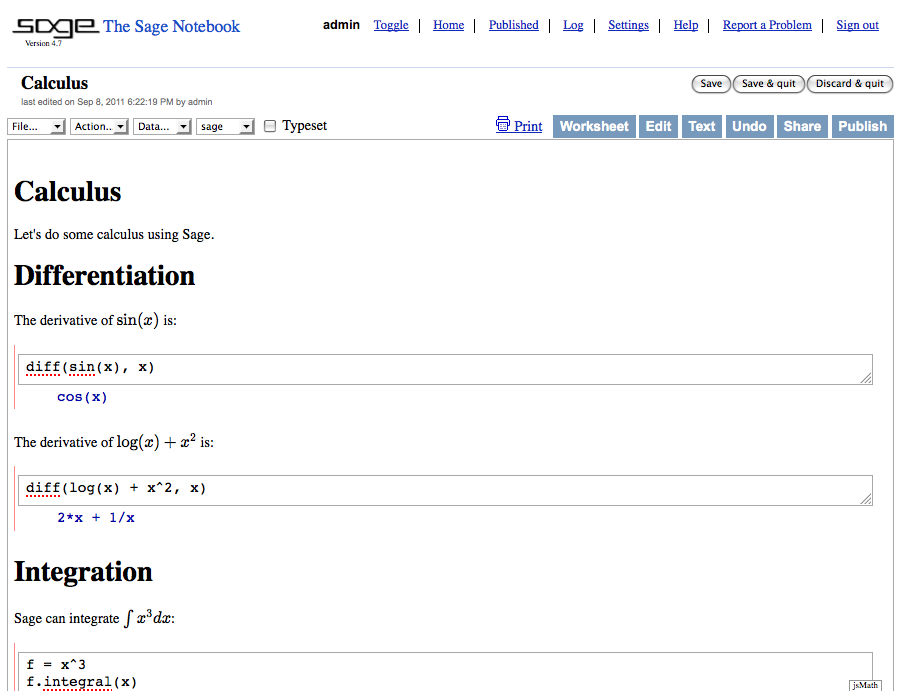
I also implemented two command line scripts to generate the worksheet text file:

sage -rst2txt file.rst file.txt

and to generate the Sage worksheet (.sws) directly:

sage -rst2sws file.rst file.sws

I also added the possibility to automatically escape every backslashes if they are not already so that they don't get lost in the translation process. For more info, consult the documentation:

sage -rst2txt -h
sage -rst2sws -h

Sage uses ReST syntax in its (Python) docstrings, but the default Python syntax highlighting in vim treats all docstrings as Python strings. Here is a method (by Franco Saliola) to enable ReST highlighting in the docstrings and highlighting of doctests.

Prerequisites

The usual syntax files python.vim and rst.vim must be in the ~/.vim/syntax folder. You can find those on the web. Here is the rst.vim file made by Nikolai Weibull (latest revision: 2010-01-23).

Configuration

Create the directory:

mkdir -p ~/.vim/after/syntax

Any file in this directory will be loaded after the default syntax files, allowing us modify the default highlighting and add our own customizations.

Copy the file python.vim (which can be found in the same directory as this file) into the directory ~/.vim/after/syntax.

The first few lines of the file python.vim define the default colours for the docstring text, the sage keywords and the sage prompt. You might want to modify these to suit your colour scheme.

References

• http://www.mail-archive.com/vim_use@googlegroups.com/msg06545.html
• help :syn-include

I just did a graph of the Evolution of the Overall Doctest Coverage of Sage since 3 years. The png is below.

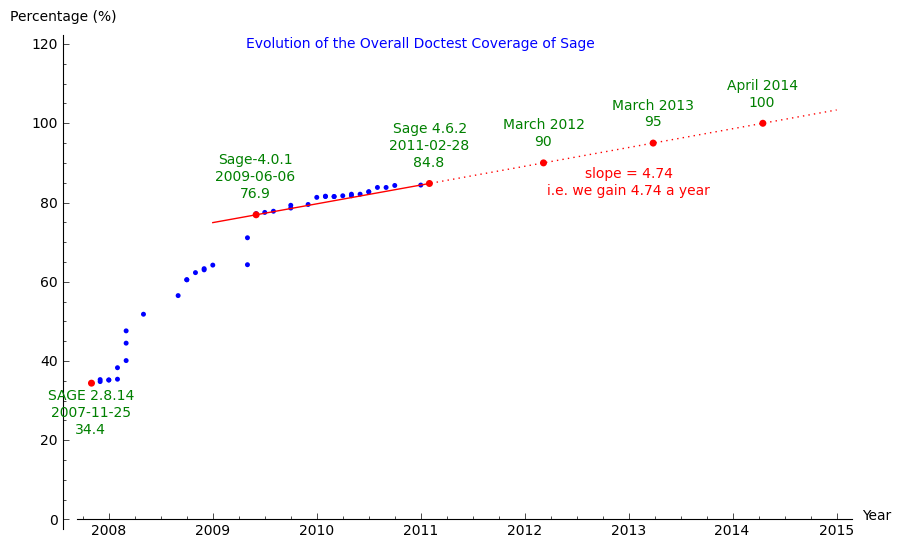
The coverage evolved quiet regularly during the last 20 releases (=20 months) with an average of a bit less than 5 percent a year. For sage-4.6.2, it is actually 84.8%. If we keep this rhythm, we should reach 90% coverage by March 2012 and 100% by April 2014.

The code I used is here : coverage_evolution.py.

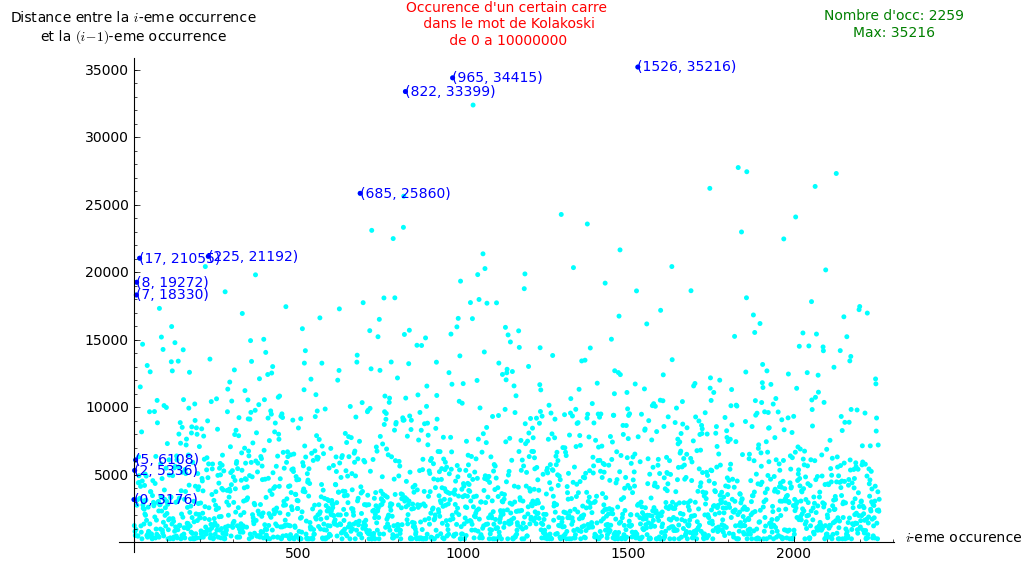
The factor 212212112112212112122112112212212112112212112122112112 occurs in the Kolakoski word at the positions 3190, 6366, 7614, 12950, 13765, 14277, 20385, 21344, 39674 and so on. The successive gaps of these first eight occurences are 3176, 1248, 5336, 815, 512, 6108, 959, 18330. Are the gap between all of these occurences bounded or not? The following table lists only the gap that are going increasingly for the Kolakoski word up to 100 billion (=10^9).

The following image draws all the gaps in function of i for the first 10 million digit.

I am currently at Sage Days 28. Right now, there is a discussion about Analytic combinatorics in Sage and the new code written by Alex Raichev at tikcet #10519 was mentionned in the discussion. His code is a bunch of def python functions in a sage file. In Sage, code is written in object oriented way.

I am not an expert of the domain of analytic combinatorics, but I am coding oriented object Python since some time now. So I wrote a comment on the ticket gathering my thoughts to, I hope, help Alex to rewrite his set of functions into an oriented object structure. I copied the content of my comment below as it will be easier to share it.

r"""
[...]

This code relates to analytic combinatorics.
More specifically, it is a collection of functions designed
to compute asymptotics of Maclaurin coefficients of certain classes of
multivariate generating functions.

The main function asymptotics() returns the first `N` terms of
the asymptotic expansion of the Maclaurin coefficients `F_{n\alpha}`
of the multivariate meromorphic function `F=G/H` as `n\to\infty`.
It assumes that `F` is holomorphic in a neighborhood of the origin,
that `H` is a polynomial, and that asymptotics in the direction of
`\alpha` (a tuple of positive integers) are controlled by smooth
or multiple points.

[...]
"""

class HolomorphicMultivariateMeromorphicFunction(object):

    # Constructor of the object
    def __init__(self, F, G):
        #stores important information on the object as attributes of self
        self._F = F
        self._G = G

    def maclaurin_coefficients(self, n, alpha):
        r"""
        Return the maclaurin coefficients of self.

        INPUT:

        - ``alpha`` - tuple of positive integers

        OUTPUT:

        a python list of the first terms

        OR

        maybe an object of a class you implement if there exists pertinent
        questions to ask to it.
        """
        #Do some computations based (I guess) on self._F and self._G
        intermediate_result1 = self.some_intermediate_computations_1()
        #Do more computations
        return something

    def asymptotics(self, N, alpha):
        r"""
        Returns the asymptotics of Maclaurin coefficients.
        """
        #Do some computations based (I guess) on self._F and self._G
        intermediate_result2 = self.some_intermediate_computations_2()
        intermediate_result3 = self.some_intermediate_computations_3()
        return something

    #put here all the others functions needed to compute the asymptotics
    def some_intermediate_computations_1(self):
        pass
    def some_intermediate_computations_2(self):
        pass
    def some_intermediate_computations_3(self):
        pass

    ...