Système de pointage proposé pour la saison 2011-2012 du Circuit québécois d'ultimate 4 contre 4
26 août 2011 | Mise à jour: 06 septembre 2011 | Catégories: ultimate, fqu | View CommentsLe système de pointage du Circuit québécois d'ultimate 4 contre 4 pour la saison 2010-2011 était le suivant:
- Série A: Movember, Bye Bye, La Flotte, Coup de Foudre, Mars Attaque
- Série B: OctoberDisk, Fun-E-nuF, La Virée
Une échelle allant de 1 à 73 points était utilisée pour les tournois de série A et donnait des points à 31 équipes. Une échelle de 1 à 16 points était utilisée pour les tournois de série B et donnait des points à 16 équipes. Ces échelles de pointages avaient été conçues à l'automne 2007 à une époque où le plus grand tournoi acceptait 36 équipes. Vu l'augmentation de popularité du circuit (le nombre d'équipes participant au circuit a doublé en trois ans), le système de pointage doit être actualisé. Notamment, sur les 88 équipes ayant participé au tournoi Mars Attaque en mars 2011, seules 31 équipes ont reçu des points et 57 équipes ont obtenu un pointage de zéro. De plus, à cause de l'ajout d'un tournoi de série A à Montréal, plusieurs équipes ont fait le choix de ne pas participer au tournoi La Flotte de Rimouski ce qui a créé un déséquilibre dans le système.
Ainsi, le système doit être actualisé pour deux raisons : (1) donner des points à toutes les équipes et (2) équilibrer le système en fonction de la force des tournois.
Plusieurs discussions ont eu lieu à ce sujet au cours des derniers mois. Certaines personnes ont suggéré de modifier complètement le système. Certains ont mentionné l'idée de ligue, etc. Dans ce message, je propose un système en continuité avec celui utilisé au cours des dernières années. À mon avis le système utilisé depuis le début va plutôt bien, on doit simplement l'actualiser.
En s'inspirant du système de l'ATP où le gagnant d'un tournoi obtient un nombre rond de points (ATP 1000 points, 2000 points, 500 points). Je propose de faire de même pour le CQU4. Ainsi, l'équipe gagnante d'un tournoi de série A obtiendra 1000 points et 400 points pour un tournoi de série B. Cinquante équipes obtiendront des points dans un tournoi de série A (sauf pour le Mars Attaque où l'échelle sera allongée) et 24 équipes obtiendront des points pour un tournoi de série B. Le tournoi La Flotte aura sa propre classe : 800 points pour l'équipe gagnante et 32 équipes obtiendront des points. Ainsi, l'équipe gagnante du tournoi La Flotte obtiendra autant de points qu'une 5e place dans un tournoi de série A ce qui correspond à la réalité. Les quatre tournois de série A seraient : Movember, Bye Bye, Coup de Foudre, Mars Attaque et les tournois de série B seraient : OctoberDisk, Fun-E-nuF, La Virée, Ottawa (nouveau) et Landaudière (nouveau). Cela est résumé dans l'image ci-bas:


Points d'esprit sportif
Trois équipes obtiennent 50 points pour les tournois de Série A et le tournoi La Flotte et une équipe obtient 50 points pour les tournois de Série B.
Somme des 3 meilleurs résultats
Pour calculer le nombre de points total d'une équipe, on fait la somme des trois meilleurs résultats comme par les années précédentes.
Les valeurs exactes des points selon les positions finales à chaque tournoi sont dans le tableau suivant.
Points par tournoi
| Position | Série A | Mars Attaque | La Flotte | Série B |
| 1 | 1000 | 1000 | 800 | 400 |
| 2 | 938 | 938 | 728 | 355 |
| 3 | 884 | 884 | 668 | 317 |
| 4 | 835 | 835 | 614 | 285 |
| 5 | 791 | 791 | 566 | 256 |
| 6 | 750 | 750 | 522 | 230 |
| 7 | 711 | 711 | 482 | 206 |
| 8 | 675 | 675 | 444 | 184 |
| 9 | 641 | 641 | 409 | 164 |
| 10 | 609 | 609 | 377 | 146 |
| 11 | 578 | 578 | 346 | 129 |
| 12 | 549 | 549 | 317 | 114 |
| 13 | 521 | 521 | 291 | 99 |
| 14 | 494 | 494 | 265 | 86 |
| 15 | 469 | 469 | 242 | 74 |
| 16 | 444 | 444 | 219 | 63 |
| 17 | 421 | 421 | 198 | 52 |
| 18 | 399 | 399 | 178 | 43 |
| 19 | 377 | 377 | 160 | 34 |
| 20 | 356 | 356 | 142 | 26 |
| 21 | 336 | 336 | 126 | 19 |
| 22 | 317 | 317 | 110 | 12 |
| 23 | 299 | 299 | 95 | 6 |
| 24 | 281 | 281 | 82 | 1 |
| 25 | 264 | 264 | 69 | 0 |
| 26 | 248 | 248 | 57 | 0 |
| 27 | 232 | 232 | 46 | 0 |
| 28 | 217 | 217 | 35 | 0 |
| 29 | 202 | 202 | 26 | 0 |
| 30 | 188 | 188 | 17 | 0 |
| 31 | 174 | 174 | 9 | 0 |
| 32 | 161 | 161 | 1 | 0 |
| 33 | 149 | 149 | 0 | 0 |
| 34 | 137 | 137 | 0 | 0 |
| 35 | 125 | 125 | 0 | 0 |
| 36 | 114 | 114 | 0 | 0 |
| 37 | 103 | 103 | 0 | 0 |
| 38 | 93 | 93 | 0 | 0 |
| 39 | 83 | 83 | 0 | 0 |
| 40 | 74 | 74 | 0 | 0 |
| 41 | 65 | 73 | 0 | 0 |
| 42 | 57 | 72 | 0 | 0 |
| 43 | 48 | 70 | 0 | 0 |
| 44 | 41 | 69 | 0 | 0 |
| 45 | 33 | 68 | 0 | 0 |
| 46 | 26 | 67 | 0 | 0 |
| 47 | 19 | 65 | 0 | 0 |
| 48 | 13 | 64 | 0 | 0 |
| 49 | 7 | 63 | 0 | 0 |
| 50 | 1 | 62 | 0 | 0 |
| 51 | 0 | 61 | 0 | 0 |
| 52 | 0 | 59 | 0 | 0 |
| 53 | 0 | 58 | 0 | 0 |
| 54 | 0 | 57 | 0 | 0 |
| 55 | 0 | 56 | 0 | 0 |
| 56 | 0 | 55 | 0 | 0 |
| 57 | 0 | 53 | 0 | 0 |
| 58 | 0 | 52 | 0 | 0 |
| 59 | 0 | 51 | 0 | 0 |
| 60 | 0 | 50 | 0 | 0 |
| 61 | 0 | 48 | 0 | 0 |
| 62 | 0 | 47 | 0 | 0 |
| 63 | 0 | 46 | 0 | 0 |
| 64 | 0 | 45 | 0 | 0 |
| 65 | 0 | 44 | 0 | 0 |
| 66 | 0 | 42 | 0 | 0 |
| 67 | 0 | 41 | 0 | 0 |
| 68 | 0 | 40 | 0 | 0 |
| 69 | 0 | 39 | 0 | 0 |
| 70 | 0 | 38 | 0 | 0 |
| 71 | 0 | 36 | 0 | 0 |
| 72 | 0 | 35 | 0 | 0 |
| 73 | 0 | 34 | 0 | 0 |
| 74 | 0 | 33 | 0 | 0 |
| 75 | 0 | 31 | 0 | 0 |
| 76 | 0 | 30 | 0 | 0 |
| 77 | 0 | 29 | 0 | 0 |
| 78 | 0 | 28 | 0 | 0 |
| 79 | 0 | 27 | 0 | 0 |
| 80 | 0 | 25 | 0 | 0 |
| 81 | 0 | 24 | 0 | 0 |
| 82 | 0 | 23 | 0 | 0 |
| 83 | 0 | 22 | 0 | 0 |
| 84 | 0 | 20 | 0 | 0 |
| 85 | 0 | 19 | 0 | 0 |
| 86 | 0 | 18 | 0 | 0 |
| 87 | 0 | 17 | 0 | 0 |
| 88 | 0 | 16 | 0 | 0 |
| 89 | 0 | 14 | 0 | 0 |
| 90 | 0 | 13 | 0 | 0 |
| 91 | 0 | 12 | 0 | 0 |
| 92 | 0 | 11 | 0 | 0 |
| 93 | 0 | 10 | 0 | 0 |
| 94 | 0 | 8 | 0 | 0 |
| 95 | 0 | 7 | 0 | 0 |
| 96 | 0 | 6 | 0 | 0 |
| 97 | 0 | 5 | 0 | 0 |
| 98 | 0 | 3 | 0 | 0 |
| 99 | 0 | 2 | 0 | 0 |
| 100 | 0 | 1 | 0 | 0 |
Classement de la saison 2010-2011 avec le système proposé
Avec le système proposé, voici le classement qu'on obtient selon les résultats de la saison 2010-2011. La colonne Variation indique le déplacement positif ou négatif en nombre de positions par rapport au classement avec le système de l'an passé. Notez que les points d'esprit sportif ne sont pas comptabilisés dans ce classement fictif.
| Position | Équipe | Points | Variation |
| 1 | Fluo Turbo Butt Bullets | 3000 | 1 |
| 2 | NINJAX | 2773 | -1 |
| 3 | Chainsaw | 2760 | 0 |
| 4 | Les Outs | 2706 | 0 |
| 5 | International | 2296 | 0 |
| 6 | Legends | 2291 | 1 |
| 7 | Petites Douceurs | 2223 | 3 |
| 8 | Les bergers de la mort | 2216 | 1 |
| 9 | Gros Mene | 2124 | 2 |
| 10 | Doc Tape | 2052 | -4 |
| 11 | Mighty Disc | 2048 | -3 |
| 12 | X-Kin (SAMBUCA) | 1923 | 1 |
| 13 | Gushmus | 1705 | 1 |
| 14 | Red Fox | 1692 | -2 |
| 15 | Sales-Add | 1548 | 0 |
| 16 | Sweet Dreams | 1407 | 4 |
| 17 | Commando | 1389 | 0 |
| 18 | Traction integrale | 1370 | 5 |
| 19 | Triangle des Bermudes | 1208 | 0 |
| 20 | Disco inferno | 1184 | -4 |
| 21 | TRUC | 1182 | 1 |
| 22 | DISKCOM | 1158 | -4 |
| 23 | Captain Morgan | 1069 | 1 |
| 24 | Tree Huckers | 1056 | -3 |
| 25 | Sugar Daddies | 1000 | 4 |
| 26 | Octopus | 973 | 0 |
| 27 | William Wallace | 951 | 5 |
| 28 | Rejected | 899 | 5 |
| 29 | TUX | 863 | -4 |
| 30 | Diskover | 810 | 1 |
| 31 | Scrat | 797 | 3 |
| 32 | Wasabi | 783 | 10 |
| 33 | FLU | 718 | 5 |
| 34 | La Galere | 675 | -7 |
| 35 | Poupix | 670 | 4 |
| 36 | Piranhas | 618 | 9 |
| 37 | Alkatraz | 616 | -1 |
| 38 | Bi-Winning | 609 | -8 |
| 39 | Morues | 603 | -11 |
| 40 | Les Garcons Perdus | 599 | 1 |
| 41 | Je m'appelle Claude | 494 | -1 |
| 42 | Rangers du Disque | 486 | 2 |
| 43 | Squeezee Lemon | 436 | 11 |
| 44 | Sunrise | 436 | 11 |
| 45 | Ta Mere | 420 | 10 |
| 46 | Mon Equipe | 402 | -3 |
| 47 | Scorsoneres | 390 | 3 |
| 48 | Disco Stu | 360 | -13 |
| 49 | Mauviettes | 356 | 4 |
| 50 | Torrents | 356 | 4 |
| 51 | Les Loups | 355 | -2 |
| 52 | Poutine | 336 | 7 |
| 53 | Squall | 333 | -7 |
| 54 | New Disc | 323 | 55 |
| 55 | Weapon of Choice | 317 | -4 |
| 56 | Road Runners Atomiques | 317 | -4 |
| 57 | Zazzle | 310 | -10 |
| 58 | Baril Poulet | 291 | -21 |
| 59 | Les Chemises Dragon | 285 | -7 |
| 60 | Nightlifes | 285 | -7 |
| 61 | Les Booms | 274 | 20 |
| 62 | Les Boudisques | 268 | 3 |
| 63 | DiskTrackFUL | 261 | 6 |
| 64 | Dispatch | 256 | -7 |
| 65 | Les Eyjafjallajokull en Eruption | 256 | -7 |
| 66 | Absolut | 245 | 14 |
| 67 | VooDoo | 238 | 10 |
| 68 | Saucez les Glosettes | 217 | 11 |
| 69 | Jordiscs | 206 | -21 |
| 70 | Mad Ployes | 206 | -21 |
| 71 | UMCE | 206 | -21 |
| 72 | Les Rene Angelil | 184 | -6 |
| 73 | Les Enfoirees de Grues | 164 | -6 |
| 74 | Whimps and Phores | 164 | -6 |
| 75 | Black Hole | 161 | 9 |
| 76 | Dix-vins | 149 | 15 |
| 77 | Weedeaters | 146 | -6 |
| 78 | Gang bang | 137 | -3 |
| 79 | Eclipse | 125 | 14 |
| 80 | Le Napolitain | 114 | -2 |
| 81 | Saimiris | 103 | 34 |
| 82 | les Blitzies | 83 | 19 |
| 83 | PFunk | 83 | 19 |
| 84 | Farfadet en furie | 80 | 10 |
| 85 | Ordehum | 79 | 28 |
| 86 | Die Gotter des Ultimate | 74 | -4 |
| 87 | UNB | 74 | -4 |
| 88 | Tony Hortons | 74 | -4 |
| 89 | Trick or Treat | 68 | 32 |
| 90 | Cobra Kai | 67 | -3 |
| 91 | Hypnos | 65 | 7 |
| 92 | Haies de Ced | 64 | 5 |
| 93 | Bretzel | 63 | -20 |
| 94 | Le Rocco | 63 | -20 |
| 95 | Now Playing | 62 | 17 |
| 96 | les Super-Genisses | 58 | 7 |
| 97 | Chummeyz | 48 | -11 |
| 98 | Diskobol | 48 | -11 |
| 99 | The Crazy 88 | 47 | 19 |
| 100 | Charettes de Plastique | 45 | -15 |
| 101 | Les Cocktails | 44 | -25 |
| 102 | Green Monster | 41 | -6 |
| 103 | Couvercles et Plats | 40 | -15 |
| 104 | Team Samoulle | 39 | 12 |
| 105 | Mobydicks | 36 | 1 |
| 106 | Nordet UQAR | 36 | 1 |
| 107 | Les Pades | 35 | -5 |
| 108 | Feu Vert | 33 | -13 |
| 109 | Mustangs | 31 | -1 |
| 110 | T-Q | 30 | 10 |
| 111 | Va comme jte pousse | 29 | 11 |
| 112 | Dislocks | 27 | -22 |
| 113 | Team Youhou! | 25 | 4 |
| 114 | Double Zebras | 24 | -22 |
| 115 | Bleu Marin | 23 | -43 |
| 116 | Chapos Poilus | 22 | -42 |
| 117 | Mr Freeze | 20 | -10 |
| 118 | Mammouths Laineux | 19 | -13 |
| 119 | Los KB | 18 | -15 |
| 120 | Nordiques | 17 | -9 |
| 121 | Juicy Pickles | 16 | -22 |
| 122 | Grues d'Acajou | 9 | -52 |
Formules
Soit \(M\) le nombre de points donnés à l'équipe gagnante d'un tournoi et soit \(N\) le nombre d'équipes à qui on donne des points. On assume que l'on donnera 1 point à la \(N\)-ième équipe. On définit les deux fonctions suivantes:
\[ F_{N}(p) = \int_p^N \log\left(\frac{\sqrt{2}N}{x}\right) dx \]
\[ G_{M,N}(p) = (M-1) \frac {F_{N}(p)} {F_{N}(1)} + 1 \]
La valeur de \(G_{M,N}(p)\) (arrondi à l'entier le plus près) est le nombre de points donnés à l'équipe terminant en position \(p\), \(1\leq p \leq N\), en fonction des paramètres \(M\) et \(N\). On remarque facilement que les deux hypothèses mentionnées ci-haut sont vérifiées: le nombre de points donnés à l'équipe gagnante est bien \(G_{M,N}(1) = M\) et le nombre de points donnés à l'équipe terminant en \(N\)-ième position est bien \(G_{M,N}(N) = 1\).
Pour les tournois de série A, les paramètres sont \(M=1000\) et \(N=50\). Pour le tournoi La Flotte, les paramètres sont \(M=800\) et \(N=32\). Pour les tournois de série B, les paramètres sont \(M=400\) et \(N=24\).
Afin de donner des points à toutes les équipes participant au tournoi Mars Attaque, on linéarise le nombre de points données à partir de la position 40 jusqu'à la dernière position (88 en 2011, 100 estimé en 2012) en donnant un point à la dernière position.
Questions à considérer
Quelques questions sont à considérer sur ce nouveau système et sur l'ultimate 4 contre 4 en général au Québec.
Question 1. Nouveaux tournois dans le circuit québécois
- Combien d'équipes participeront aux nouveaux tournois d'Ottawa et de Lanaudière?
- Quelle force donnera-t-on à ces deux nouveaux tournois (Série A, Série B, intermédiaire)?
Quelques autres propositions:
Question 2. Envergure du Championnat québécois 4 contre 4
Le Championnat québécois d'ultimate 4 contre 4 (où sont invitées les 16 meilleures équipes au classement) manque d'envergure. Il y a peu de spectateurs. C'est une opportunité perdue pour la promotion du sport. Comment augmenter son envergure?
Voici des solutions non exclusives:
- Organiser un Beginner's Luck en parallèle.
- Faire des ateliers pour les juniors.
- Inviter le 17-32 au Championnat québécois dans un tournoi parallèle.
- Inviter le top 8 des meilleures équipes junior du circuit et faire un Championnat junior 4 contre 4
Question 3. Règles du jeu du 4 contre 4
Temps morts dans les 5 dernières minutes. Veut-on faire comme à Paganello?
CQU4 au Québec: Revirement
À Paganello: reprise du jeu, validation sur compte + 2 (maximum 9)
Il faudrait aussi Faire les améliorations proposées (de forme) par Lorne Beckman il y a bientôt deux ans.
Question 4. Règlements sur l'alignement
Doit-on alléger ou modifier les règles sur l'alignement des équipes spécialement pour le Championnat québécois 4 contre 4?
Tous les joueurs d'une équipe qui participent au Championnat québécois 4 contre 4 doivent avoir joué à au moins deux tournois avec cette équipe au cours de la saison.
En effet, les demandes de dérogation au réglement génère trop de gestion administrative et d'énergie perdue.
Question 5. Les finales du dimanche
Veut-on suivre le modèle Mars Attaque 2010? C'est-à-dire devancer la finale pour que ça ne soit pas le dernier match du tournoi.
Question 6. Autres modifications (de forme) des Règlements du circuit
Dans la section "Critères d’organisation d’un tournoi du circuit (A et B)", fusionner la partie série A et série B.
Dans la section "Critères d’organisation d’un tournoi du circuit (A et B)", modifier
Remettre à la FQU le classement final et complet des équipes de même que le top 3 de l'esprit sportif voté par les équipes participantes;
par
Remettre à la FQU le classement final et complet des équipes avec la ville de provenance de même que le top 3 de l'esprit sportif voté par les équipes participantes;
Dans la section "Responsabilité de la FQU", ajouter "Déléguer la sélection aux associations".
Fusionner les formulaires à la fin du document pour la série A et B qui sont presque identique en ajoutant une case à cocher : Série A ou Série B.
Animation des solutions d'un puzzle de Florent Hivert
22 juillet 2011 | Catégories: animation, sage | View CommentsOn veut placer les pièces suivantes dans un carré 8 par 8.
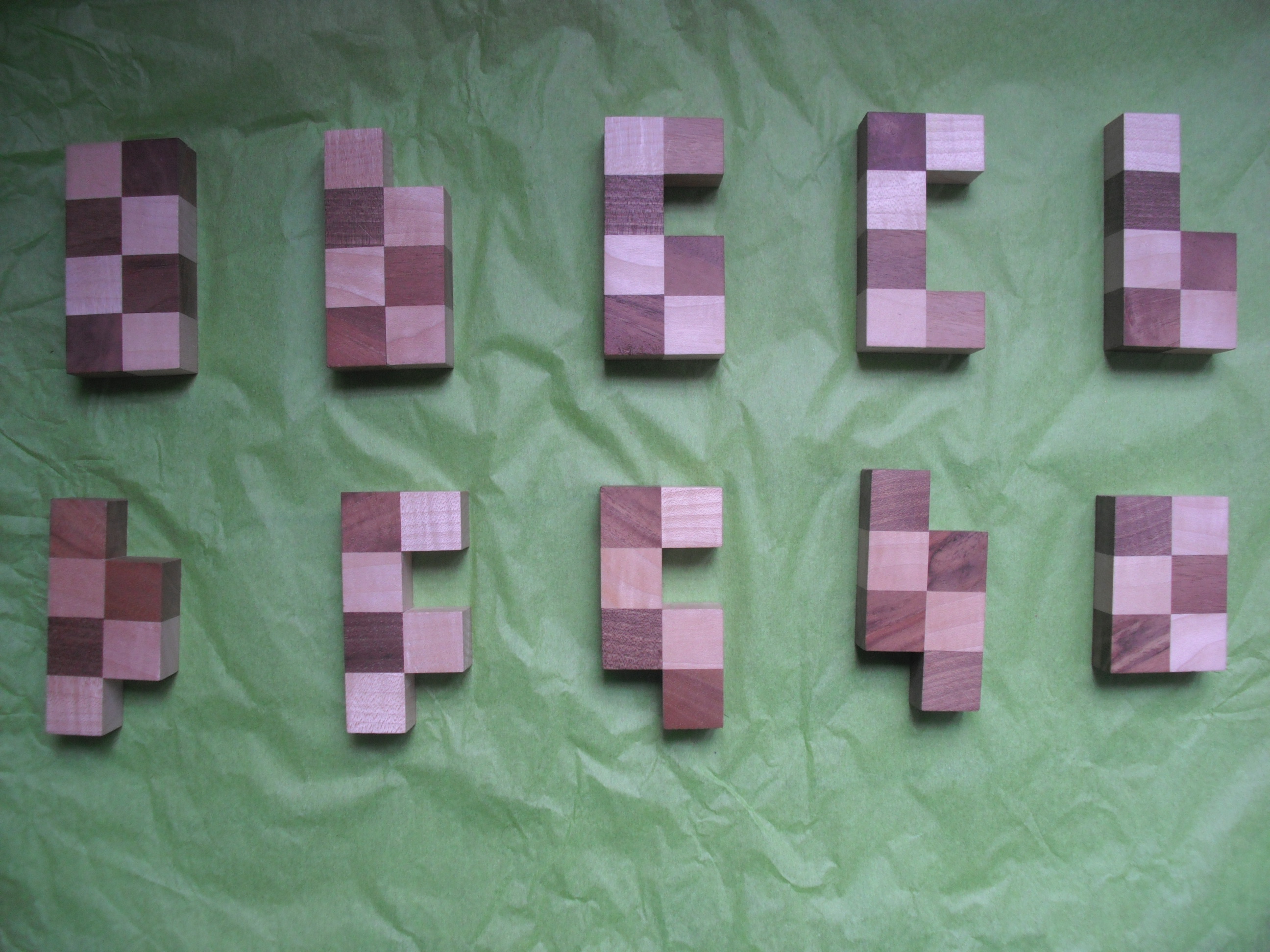
En utilisant sage-4.7 muni des patchs du ticket #11379 et avec les commandes suivantes, on peut trouver une solution et même les calculer toutes:
sage: from sage.combinat.tiling import Polyomino, TilingSolver sage: L = [] sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3)], 'yellow')) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2)], "black")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,3)], "gray")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,3)],"cyan")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1)],"red")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,1),(1,2)],"blue")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,1),(1,3)],"green")) sage: L.append(Polyomino([(0,1),(0,2),(0,3),(1,0),(1,1),(1,3)],"magenta")) sage: L.append(Polyomino([(0,1),(0,2),(0,3),(1,0),(1,1),(1,2)],"orange")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(1,0),(1,1),(1,2)],"pink")) sage: T = TilingSolver(L, (8,8), reflection=True) sage: T.number_of_solutions() 328
Ainsi (sans tenir compte de la non adjacence des carrés blancs et noirs), il y a 328 solutions. Les voici en animation:
sage: a = T.animate() sage: a Animation with 328 frames sage: a.show(delay=50, iterations=1)

Chaque solution est répétée 8 fois (les 4 rotations et les 4 rotations de l'image miroir), ainsi il n'y a que 41 solutions vraiment distinctes:
sage:: factor(328) 8 * 41
J'ai aussi codé:
sage: a = T.animate('incremental', stop=300)
où une seule pièce est enlevée ou ajoutée à la fois ce qui permet vraiment de visualiser les liens dansants de Knuth (rafraîchir le navigateur pour faire recommencer l'animation):

ReST to Sage Worksheet
17 juin 2011 | Mise à jour: 08 septembre 2011 | Catégories: rst, sage | View CommentsDuring Sage Days 31, I worked on the ticket #11459 to implement rst to sws conversion. This post intends to give some documentation about this new feature. Here is an example of a ReStructuredText file calculus.rst:
********
Calculus
********
Let's do some calculus using Sage.
Differentiation
===============
The derivative of $\\sin(x)$ is::
sage: diff(sin(x), x)
cos(x)
The derivative of $\\log(x) + x^2$ is::
sage: diff(log(x) + x^2, x)
2*x + 1/x
Integration
===========
Sage can integrate $\\int x^3 dx$::
sage: f = x^3
sage: f.integral(x)
1/4*x^4
Let's compute $\\int x \\sin(x^2) dx$::
sage: f = x*sin(x^2)
sage: integral(f,x)
-1/2*cos(x^2)
Both the files calculus.rst and calculus.html, which was generated from the file calculus.rst using Docutils and the command rst2html.py calculus.rst calculus.html, can be uploaded into the Sage Notebook (copy their URL):
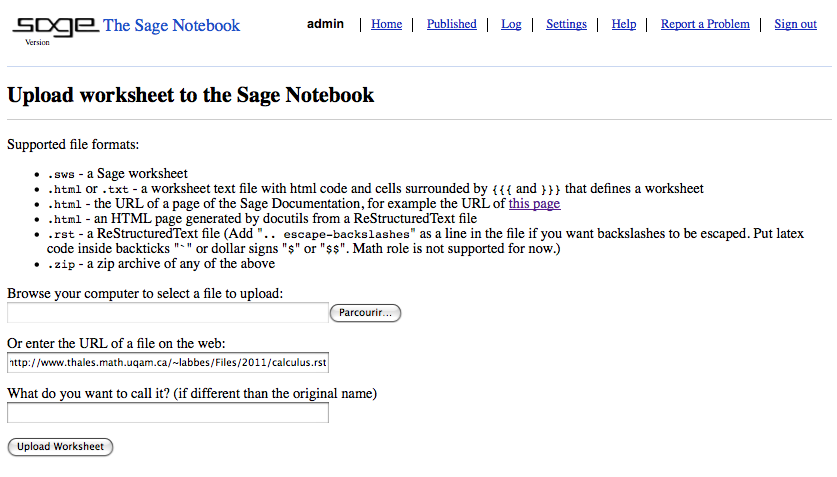
This will create a new worksheet:
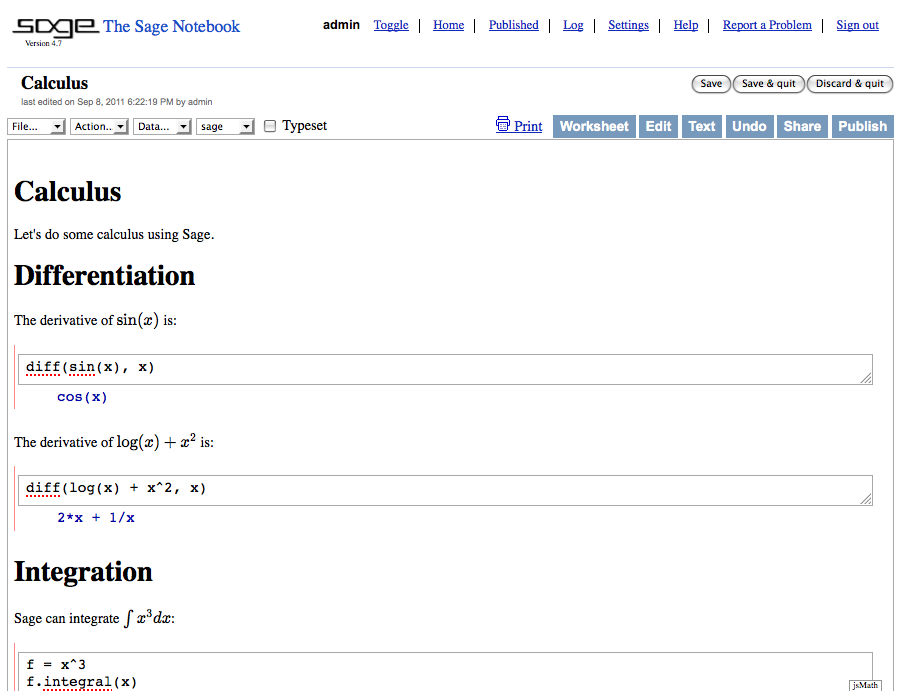
I also implemented two command line scripts to generate the worksheet text file:
sage -rst2txt file.rst file.txt
and to generate the Sage worksheet (.sws) directly:
sage -rst2sws file.rst file.sws
I also added the possibility to automatically escape every backslashes if they are not already so that they don't get lost in the translation process. For more info, consult the documentation:
sage -rst2txt -h sage -rst2sws -h
ReST syntax highlighting for Sage docstrings in VIM
15 juin 2011 | Catégories: sage | View Comments| Author: | Franco Saliola |
|---|---|
| Contact: | saliola at gmail dot com |
| Date: | 3 December 2010 |
Sage uses ReST syntax in its (Python) docstrings, but the default Python syntax highlighting in vim treats all docstrings as Python strings. Here is a method (by Franco Saliola) to enable ReST highlighting in the docstrings and highlighting of doctests.
Prerequisites
The usual syntax files python.vim and rst.vim must be in the ~/.vim/syntax folder. You can find those on the web. Here is the rst.vim file made by Nikolai Weibull (latest revision: 2010-01-23).
Configuration
Create the directory:
mkdir -p ~/.vim/after/syntax
Any file in this directory will be loaded after the default syntax files, allowing us modify the default highlighting and add our own customizations.
Copy the file python.vim (which can be found in the same directory as this file) into the directory ~/.vim/after/syntax.
The first few lines of the file python.vim define the default colours for the docstring text, the sage keywords and the sage prompt. You might want to modify these to suit your colour scheme.
References
- http://www.mail-archive.com/vim_use@googlegroups.com/msg06545.html
- help :syn-include
Suivre l'évolution d'un match d'ultimate point par point
19 avril 2011 | Catégories: ultimate | View CommentsDans un tournoi et surtout dans une saison, on joue plusieurs parties, alors il est facile d'oublier le déroulement des parties jouées et du même coup les leçons qu'on y a faites. Cette saison, l'équipe Odyssée utilisera une méthode facile et innovatrice afin d'archiver les parties jouées et ainsi avoir un support visuel pour se rappeler de celles-ci, de leur déroulement et surtout des erreurs à ne pas refaire et des bons coups à répéter. La méthode est de remplir une grille d'évolution des matchs jouées où on encercle simplement le pointage en cours. Par exemple, voici la grille d'évolution de la finale du CQU4 Ninjax vs Bergers tenue en avril dernier :
- Bergers vs Ninjax, finale du CQU4 2011

Comme vous voyez, en un coup d'oeil, la grille réussit bien à se rappeler le cours du match ou même à quelqu'un qui n'a pas vu le match d'avoir une bonne idée de l'allure du match. La grille permet de dire plus. Par exemple, elle permet de déterminer le nombre de fois qu'une équipe se fait briser : il suffit de calculer la longueurs des plateaux horizontaux et verticaux. Les Bergers se sont faits briser 8 fois de suite 3-3 à 11-3 ce qui a été fatal. Par la suite, la pente illustre qu'il y a eu un certain retour dans le match de la part des Bergers mais jamais assez pour retoucher à la diagonale ou autrement dit à revenir à égalité avec Ninjax.
Voici la grille montrant l'évolution de la finale division masculine des Championnats canadiens d'ultimate (CUC) 2010:
- Méphisto vs Moodooggies, finale division masculine, CUC 2010
Les grilles vierges que nous utiliserons au cours de la saison sont les suivantes (en format pdf):
« Previous Page -- Next Page »
